import numpy as np
import matplotlib.pyplot as pltMedian & Streudiagramm
Ähnlich wie im vorangegangenen Kapitel soll nicht angenommen werden, dass Mediane und Streudiagramme zusammengehören - sie werden hier aber zusammen eingeführt.
Median
Der Median (auch: Zentralwert) ist dem Mittelwert insofern ähnlich, als dass er auch ein Lagemaß für die Mitte der Daten ist. Im Gegensatz zum Mittelwert wird er aber nicht wirklich berechnet, sondern wird sozusagen herausgesucht, da es der Wert ist, der genau in der Mitte aller sortierten Werte liegt. Das bedeutet, dass die Hälfte aller Werte kleiner und die andere Hälfte aller Werte größer als der Median sind. Streng genommen funktioniert das nur bei einer ungeraden Anzahl von Werten. Bei einer geraden Anzahl von Werten wird der Median deshalb als arithmetischer Mittelwert der beiden mittleren Werte berechnet:

Quelle: Wikipedia
Eine Eigenschaft des Medians ist, dass er im Vergleich zum arithmetischen Mittelwert robuster gegenüber Ausreißern ist. Das bedeutet, dass ein oder zwei extrem hohe oder niedrige Werte den Median nicht so stark beeinflussen wie den Mittelwert. Das ist nicht unbedingt immer ein Vorteil, kann aber in manchen Fällen durchaus zielführend sein. Als Beispiel wollen wir wieder Noten von Personen heranziehen:
noten_C = np.array([1, 2, 2, 2, 1, 2, 1, 1])
mw_C = np.mean(noten_C)
median_C = np.median(noten_C)
print(mw_C)
print(median_C)1.5
1.5noten_D = np.array([1, 1, 1, 1, 1, 1, 1, 5])
mw_D = np.mean(noten_D)
median_D = np.median(noten_D)
print(mw_D)
print(median_D)1.5
1.0Wieder gilt, dass beide Personen gleich viele Noten bekommen haben. Person C hat aber nur und gleich oft die Noten 1 und 2 bekommen, während Person D mit Ausnahme einer 5 ausschließlich 1en bekommen hat. Wieder haben beide Personen im Durchschnitt die gleiche Note (= 1,5), aber der Median von Person Person C ist 1,5 - also identisch zum Mittelwert - wohingegen der Median von Person D 1,0 ist.
Das zeigt, dass der Median in diesem Fall also weniger von der 5 beeinflusst wird als der Mittelwert. Wie gesagt ist das nicht unbedingt besser oder richtiger. Natürlich ist die Note 5 eben eine Note 5 und soll nicht unter den Teppich gekehrt werden. Auf dem Zeugnis steht letztendlich der Notenschnitt und nicht der Notenmedian. Dennoch vermittelt der Median in diesem Szenario eine Zusatzinformation, die Person D wohl auch etwa so erwähnen würde, wenn sie zu Wort käme: “Ja, aber ich habe eigentlich nur nur 1en, habe aber leider einmal eine 5 bekommen.”
Wir können nochmal ein Histogramm zeichnen, um das zu veranschaulichen. Da wir diesmal aber sowohl den Mittelwert, als auch den Median einzeichnen wollen, nehmen wir folgende Änderungen im Vergleich zu den Histogrammen im letzten Kapitel vor:
- Wir nutzen
plt.axvline()zwei Mal, um sowohl den Mittelwert, als auch den Median einzuzeichnen. Dabei stellen wir sicher, dass die Linien unterschiedlich aussehen, indem wir die Farbe und den Linienstil anpassen. - Wir ergänzen eine Notiz, die erklärt welche Linie was darstellt. Eine Möglichkeit ist, dies in den Untertitel zu schreiben. Tatsächlich gibt es keine Funktion, die ohne Weiteres einen Untertitel unterhalbt von
plt.title()hinzu fügt. Wir können aber die Funktionplt.suptitle()verwenden, welche sozusagen eine Übertitel oberhalb einfügt. Somit setzen wir die Bezeichnung der Person alsplt.suptitle()und die Erklärung der Linien alsplt.title(), wobei wir bei letzterem noch das Argumentfontsizenutzen um die Schriftgröße zu reduzieren. - Wir nehmen andere Füllfarben als für Person A und B.
- Wir passen die Limits der y-Achse an, da die Anzahl der Noten zumindest von Person D diesmal höher ist.
noten_bins = [0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5]
untertitel = 'Die gestrichelte rote Linie zeigt den Mittelwert und die gepunktete blaue Linie den Median.'plt.figure()
plt.suptitle('Person C')
plt.title(untertitel, fontsize=7)
plt.hist(
noten_C,
bins=noten_bins,
color='plum',
edgecolor='black'
)
plt.axvline(
mw_C,
color='red',
linestyle='dashed'
)
plt.axvline(
median_C,
color='blue',
linestyle='dotted'
)
plt.xlabel('Noten')
plt.ylabel('Anzahl')
plt.ylim(0, 7.5)
plt.show()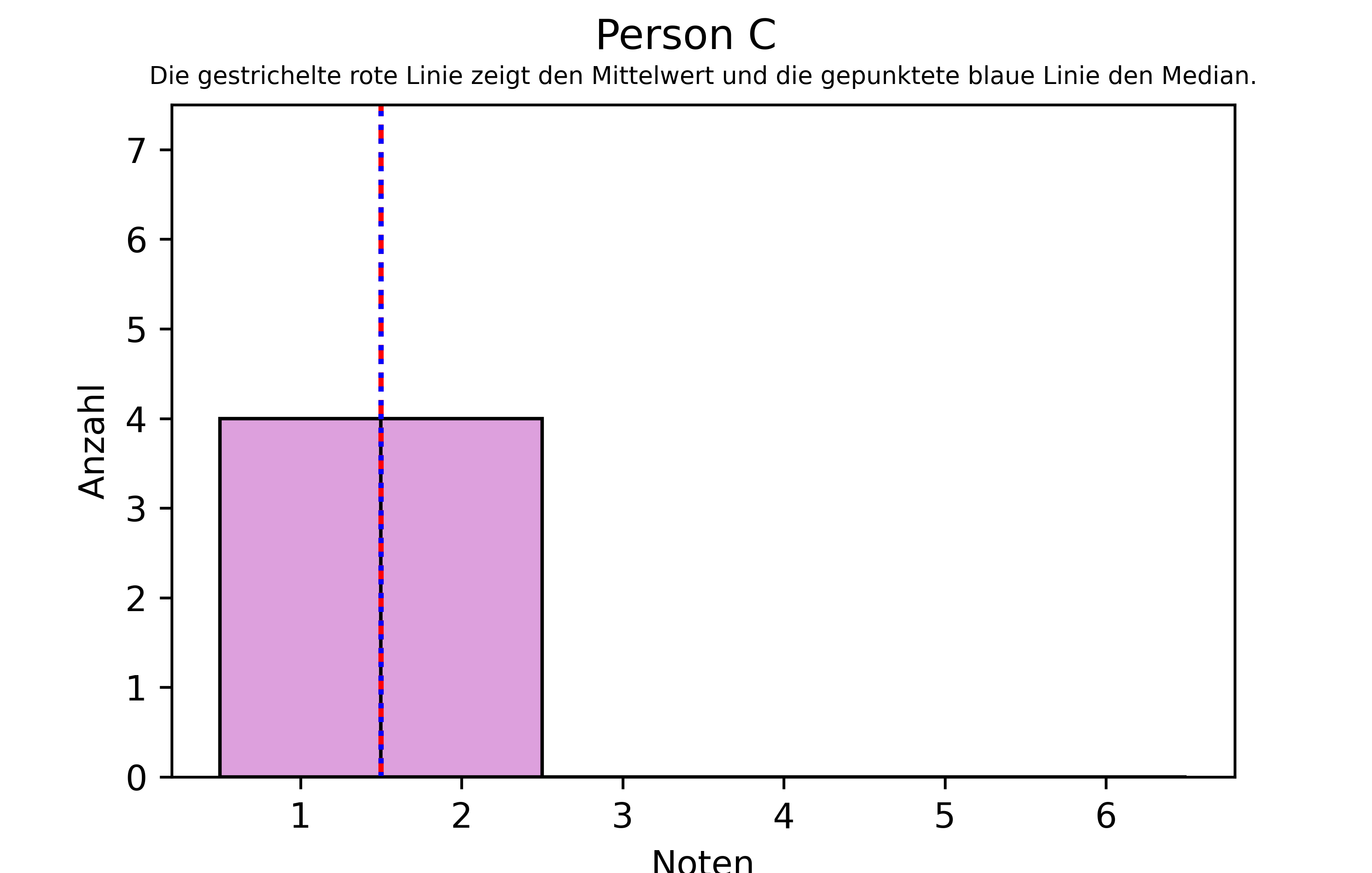
plt.figure()
plt.suptitle('Person D')
plt.title(untertitel, fontsize=7)
plt.hist(
noten_D,
bins=noten_bins,
color='palegreen',
edgecolor='black'
)
plt.axvline(
mw_D,
color='red',
linestyle='dashed'
)
plt.axvline(
median_D,
color='blue',
linestyle='dotted'
)
plt.xlabel('Noten')
plt.ylabel('Anzahl')
plt.ylim(0, 7.5)
plt.show()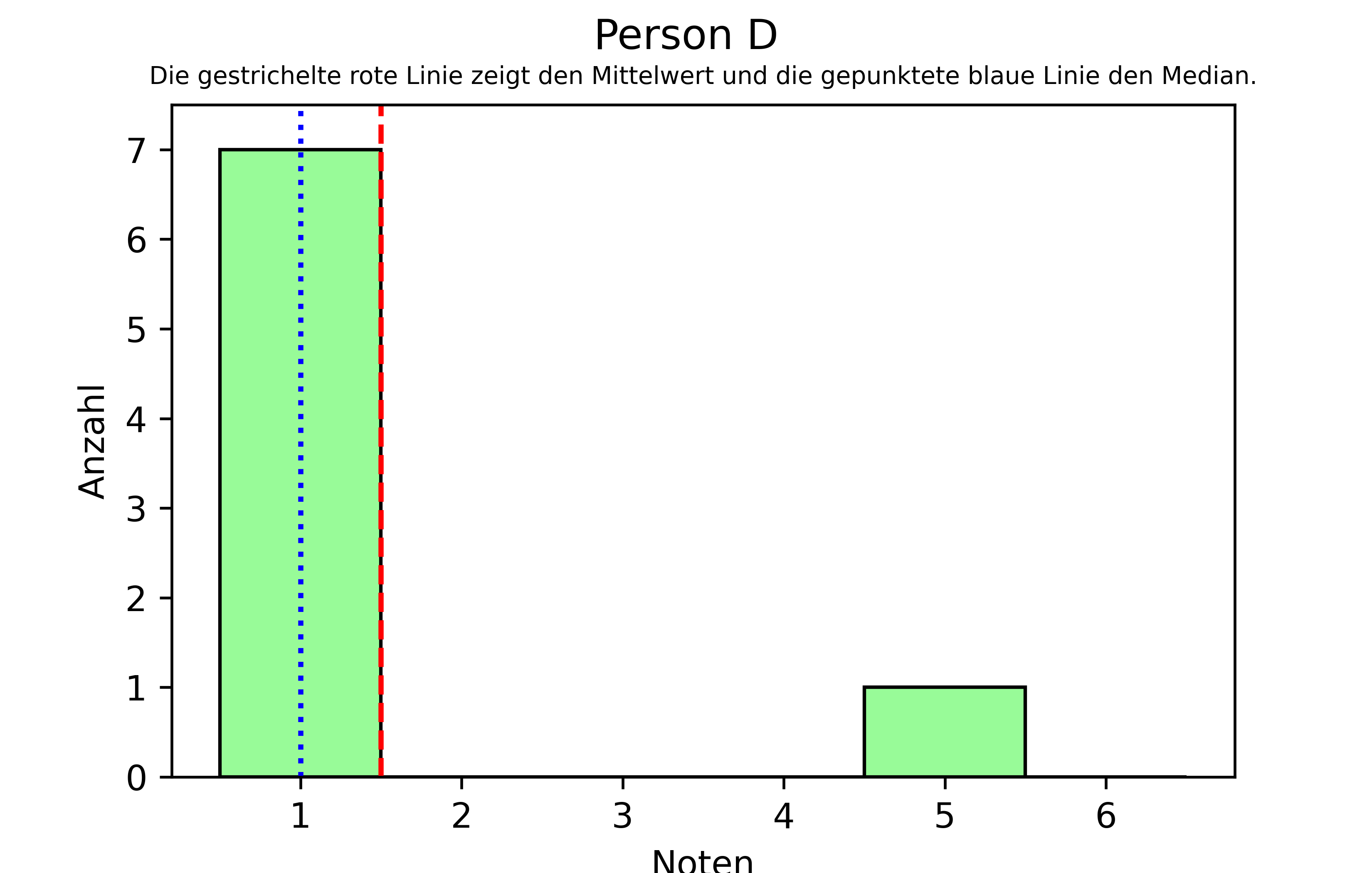
Weitere
Am Ende sei hier noch erwähnt, dass hin und wieder auch der Modus (auch: Modalwert) und die Spannweitenmitte (auch: mid-range) als Lagemaß genannt werden. Beide können in manchen Fällen durchaus sinnvoll sein, werden aber in der Regel nicht so häufig verwendet wie der Median und der Mittelwert.
Der Modus ist der Wert, der am häufigsten in einer Datenmenge vorkommt. Tatsächlich gibt es weder in Standard-Python, noch in numpy eine Funktion um dem Modus zu berechnen1.
Die Spannweitenmitte ist der Mittelwert aus dem kleinsten (Minimum) und größten (Maximum) Wert einer Datenmenge. Hier gibt es ebenfalls keine Funktion in Standard-Python oder numpy, allerdings kann die Spannweite ja mit numpy Funktionen berechnet werden als (np.min(data) + np.max(data)) / 2 oder als np.mean([np.min(data), np.max(data)]).
- Lagemaße [nur bis zur Überschrift “Lagemaße mit DATAtab berechnen” und ohne die enthaltenen Videos]
Übungen
Analysiere mittels Histogramm und Mittelwert/Median die Wohnungsgrößen in einem imaginären Stadtteil. Alle Quadratmeterzahlen je Wohnung sind in der Liste qm gespeichert. Als Hilfestellung sind zusätzlich Intervalle/bins für das Histogramm in dem Array Liste qm_bins gespeichert, probiere aber ruhig ein paar andere aus.
qm = [ 56.8, 52.8, 71.6, 89.2, 47.5, 70.7, 78.9, 58.6, 56.4, 85.3, 72.5, 79.6, 58.4, 92. , 960.1, 74.8, 87. , 66.8, 58.9, 58.8, 85.5, 46.5, 49.7, 10.2, 101.2, 95.9, 30.7, 91.6, 60.8, 85.5]
qm_bins = np.arange(0, 1025, 25)Jeweils angegeben/gerundet als ganze Zahl (ohne Nachkommastellen),
Wie viele Wohnung gibt es?
Wie groß ist eine Wohnung im Mittel?
Wie groß ist eine Wohnung im Median?: