Sets

Material

Woche 2

Zuletzt aktualisiert

9. Oktober 2025

Der dritte Typ von Sammlungen in Python sind Sets. Auch Sets sind Listen sehr ähnlich: Sie sind nicht homogen, Verschachtelungen sind möglich und sie sind mutable. Sets unterscheiden sich aber auch von Listen: Sie sind nicht geordnet, erlauben keine Duplikate und werden mit geschweiften Klammern {} erstellt.

’

Eigenschaft	Liste	Tuple	Set	Dictionary
Darstellung	[ ]	( )	{ }	{ }
Beispiel	[1, 2, 2, 'drei']	(1, 2, 2, 'drei')	{'drei', 1, 2}	{1: 'a', 2: 'b', 3: 'b', 'drei': 'c'}
Homogenität	Nicht-homogen	Nicht-homogen	Nicht-homogen	Nicht-homogen
Verschachtelung möglich	Ja	Ja	Ja	Ja
Geordnet	Ja	Ja	Nein	Ja (Python 3.7+)
Duplikate erlaubt	Ja	Ja	Nein	Nein (nur Werte)
Mutability	{{< fa chalkboard >}} Mutable	{{< fa print >}} Immutable	{{< fa chalkboard >}} Mutable	{{< fa chalkboard >}} Mutable
Erstellung aus x	list(x)	tuple(x)	set(x)	dict(x)
Erstellung leer	[]	()	set()	{}

’

Arbeiten mit Sets

Erstellen

Sets können prinzipiell auf die gleiche Weise wie Listen erstellt werden. Allerdings fällt hier direkt auf, dass die doppelte 42 beim Erstellen des Sets einfach verschwindet. Das liegt daran, dass Sets keine Duplikate erlauben.

mein_set = {'Etwas', 42, 'Text', 42, 12.6, True}
mein_set

{'Text', True, 'Etwas', 42, 12.6}

zahlen_set = {1, 6, 3, 2}
sum(zahlen_set)

Listen/Tuples können auch in Sets umgewandelt werden und umgekehrt. Dabei wird die ursprüngliche Sammlung nicht verändert, sondern eine neue Sammlung erstellt. Das Umwandeln z.B. einer Liste in ein Set ist auch eine gängige Methode, um Duplikate zu entfernen.

alle_namen = ['Goku', 'Vegeta', 'Goku', 'Goku', 'Gohan', 'Vegeta']
einzigartige_namen = set(alle_namen)
print(alle_namen)

['Goku', 'Vegeta', 'Goku', 'Goku', 'Gohan', 'Vegeta']

print(einzigartige_namen)

{'Gohan', 'Goku', 'Vegeta'}

x = {1, 2, 3}
y = list(x)
print(x)

{1, 2, 3}

print(y)

[1, 2, 3]

Hinzufügen

Anstellen von append() oder insert() wie bei Listen gibt es bei Sets die Methode add(). Diese fügt ein Element hinzu, falls es noch nicht im Set enthalten ist. Falls es bereits enthalten ist, passiert nichts.

x = {1, 2, 3}
x.add(4)
x

{1, 2, 3, 4}

Entfernen

Anstellen von remove() wie bei Listen gibt es bei Sets die Methoden discard() und remove(). Diese entfernt ein Element, falls es im Set enthalten ist. Falls es nicht enthalten ist, passiert nichts. Beide Methoden unterscheiden sich nur darin, dass remove() einen Fehler wirft, falls das Element nicht enthalten ist, während discard() dann einfach nichts tut.

x = {1, 2, 3}
x.discard(3)
x

{1, 2}

x = {1, 2, 3}
x.discard(4)
x

{1, 2, 3}

x = {1, 2, 3}
x.remove(3)
x

{1, 2}

x = {1, 2, 3}
x.remove(4)
#

Error: 4

Es gibt wie auch bei Listen die Methode pop(). Allerdings wird hier nicht wie bei Listen immer das letzten Element entfernt, sondern ein zufälliges. Das liegt daran, dass Sets ja nicht geordnet sind, sodass es sozusagen kein “letztes” Element gibt.

Auch die Methode clear() funktioniert wie bei Listen und entfernt alle Elemente aus dem Set.

Set-Operationen

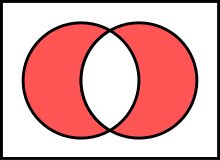
Sets haben auch spezielle Methoden, die Listen und Tuples nicht haben. Diese eignen sich speziell für Mengenoperationen von Daten ohne Duplikate. Set bedeutet im englischen ja auch “Menge” im mathematischen Sinne. Mengenoperationen sind z.B. Vereinigung, Schnittmenge und Differenz und ihr Konzept wird beispielsweise bei Venn-Diagrammen wie diesem hier angesetzt:

Die wichtigsten Mengenoperationen werden hier kurz vorgestellt. Es sei darauf hingewiesen, dass hier immer nur mit zwei Sets (x und y) gearbeitet wird, aber die Methoden i.d.R. auch mit mehreren Sets funktionieren.

Union (Vereinigung)

Sets können vereinigt werden, d.h. es werden alle Elemente beider Sets in einem neuen Set zusammengefasst. Das geht entweder via union() oder |.

x = {1, 2}
y = {2, 3}

z = x.union(y)

print(x)

{1, 2}

print(y)

{2, 3}

print(z)

{1, 2, 3}

x = {1, 2}
y = {2, 3}

z = x | y

print(x)

{1, 2}

print(y)

{2, 3}

print(z)

{1, 2, 3}

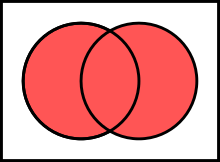
Der Unterschied ist, dass union() auch andere Sammlungen (Listen, Tuples…) akzeptiert und automatisch in Sets umwandelt, während | nur Sets akzeptiert.

Intersection (Schnittmenge)

Sets können auch geschnitten werden, d.h. es werden nur die Elemente in einem neuen Set zusammengefasst, die in beiden Sets enthalten sind. Das geht entweder via intersection() oder &.

x = {1, 2}
y = {2, 3}

z = x.intersection(y)

print(x)

{1, 2}

print(y)

{2, 3}

print(z)

{2}

x = {1, 2}
y = {2, 3}

z = x & y

print(x)

{1, 2}

print(y)

{2, 3}

print(z)

{2}

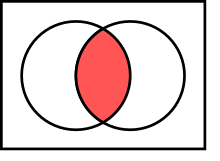
Wieder ist der Unterschied, dass intersection() auch andere Sammlungen (Listen, Tuples…) akzeptiert und automatisch in Sets umwandelt, während & nur Sets akzeptiert. Oft reicht bereits die Information, ob es überhaupt Elemente in der Schnittmenge gibt, und nicht die Schnittmenge selbst. Für diesen Fall gibt es die Methode isdisjoint(), die True zurückgibt, falls keine Elemente in der Schnittmenge sind.

x = {1, 2}
y = {2, 3}

x.isdisjoint(y)

False

x = {1, 2}
y = {3, 4}

x.isdisjoint(y)

True

Difference

Sets können auch voneinander abgezogen werden, d.h. es werden nur die Elemente in einem neuen Set zusammengefasst, die in einem Set enthalten sind, aber nicht im anderen. Das geht entweder via difference() oder -.

x = {1, 2}
y = {2, 3}

z = x.difference(y)

print(x)

{1, 2}

print(y)

{2, 3}

print(z)

{1}

x = {1, 2}
y = {2, 3}

z = x - y

print(x)

{1, 2}

print(y)

{2, 3}

print(z)

{1}

Symmetric Difference

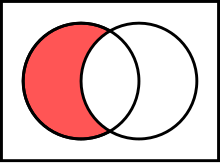
Sets können auch symmetrisch voneinander abgezogen werden, d.h. es werden nur die Elemente in einem neuen Set zusammengefasst, die in einem Set enthalten sind, aber nicht im anderen. Das geht entweder via symmetric_difference() oder ^.

x = {1, 2}
y = {2, 3}

z = x.symmetric_difference(y)

print(x)

{1, 2}

print(y)

{2, 3}

print(z)

{1, 3}

x = {1, 2}
y = {2, 3}

z = x ^ y

print(x)

{1, 2}

print(y)

{2, 3}

print(z)

{1, 3}

Subset/Superset

Schließlich kann es auch von Interesse sein zu prüfen ob ein Set ein Subset (Teilmenge) oder Superset (Obermenge) eines anderen Sets ist. Das geht entweder via issubset() oder </<= bzw. issuperset() oder >/>=.

x = {1}
y = {1, 2}

print(x.issubset(y))

True

print(x <= y)

True

print(x < y)

True

x = {1, 2}
y = {1, 2}

print(x.issubset(y))

True

print(x <= y)

True

print(x < y)

False

x = {1, 2}
y = {1, 2}

print(x.issuperset(y))

True

print(x >= y)

True

print(x > y)

False

x = {1, 2}
y = {1}

print(x.issuperset(y))

True

print(x >= y)

True

print(x > y)

True

Übungen

Erzeuge dir folgende Liste: liste = ['BMW', 'Audi', 'Mercedes', 'VW', 'Porsche', 'Audi', 'BMW']. Nutze die Funktionalität von Sets, um die Liste durch Umwandlung in ein Set von Duplikaten zu befreien. Sorge danach dafür, dass das Ergebnis aber wieder in einer Liste (und nicht eine Set) vorliegt und alphabetisch sortiert ist.

Geschafft

Prüfe ob bzw. welche der folgenden Tuples bzgl. ihrer einzigartigen Elemente Subsets der anderen sind:

id_kunden_alle = (
    536, 731, 844, 226, 463, 60, 649, 242, 893, 364, 773, 509, 536, 548, 248, 104, 816, 479,
    866, 67, 652, 695, 873, 247, 185, 46, 973, 537, 403, 109, 618, 491, 129, 450, 279, 701,
    742, 615, 92, 672, 799, 90, 695, 99, 325, 618, 136, 26, 183, 761, 843, 788, 415, 655,
    202, 203, 354, 411, 727, 131, 513, 120, 631, 202, 603, 312, 104, 635, 880, 823, 126, 471,
    89, 278, 564, 215, 42, 889, 768, 155, 384, 555, 477, 122, 383, 965, 954, 360, 549, 560,
    699, 935, 743, 585, 165, 421, 736, 908, 46, 17
)

id_kunden_positives_feedback = (247, 185, 46, 973, 537, 403, 109, 618, 491, 129, 450, 279, 701,
    742, 615, 92, 672, 799, 90, 695, 99, 325, 618, 136, 26, 183, 761, 843, 788, 415, 655,
    202, 203, 354, 411, 727, 131, 513, 120, 631, 202, 603, 312, 104, 635, 880, 823, 126, 471,
    89, 278, 564, 215, 42, 889, 768, 155, 384, 555, 477, 122, 383, 965, 954, 360, 549, 560,
    699, 935, 743, 585, 165, 421, 736, 247, 185, 46, 973, 537, 403, 247, 185, 46, 973, 537, 403,
    247, 185, 46, 973, 537, 403, 247, 185, 46, 973, 537, 403, 247, 185, 46, 973, 537, 403
)

id_kunden_gekuendigt = (731, 743, 585)

Geschafft

--- title: Sets author: "Woche 2" --- Der dritte Typ von Sammlungen in Python sind Sets. Auch Sets sind Listen sehr ähnlich: Sie sind nicht homogen, Verschachtelungen sind möglich und sie sind {{< fa chalkboard >}} mutable. Sets unterscheiden sich aber auch von Listen: Sie sind nicht geordnet, erlauben keine Duplikate und werden mit geschweiften Klammern `{}` erstellt. ```{python} #| echo: false from utils import * ``` ::: {.content-visible when-format="html"} ```{python} #| echo: false #| results: asis datstr.to_html(index=False) ``` ::: ::: {.content-visible when-format="pdf"} ```{python} #| echo: false #| results: asis datstr ``` ::: # Arbeiten mit Sets ## Erstellen Sets können prinzipiell auf die gleiche Weise wie Listen erstellt werden. Allerdings fällt hier direkt auf, dass die doppelte 42 beim Erstellen des Sets einfach verschwindet. Das liegt daran, dass Sets keine Duplikate erlauben. :::: {.grid} ::: {.g-col-6} ```{python} mein_set = {'Etwas', 42, 'Text', 42, 12.6, True} mein_set ``` ::: ::: {.g-col-6} ```{python} zahlen_set = {1, 6, 3, 2} sum(zahlen_set) ``` ::: :::: Listen/Tuples können auch in Sets umgewandelt werden und umgekehrt. Dabei wird die ursprüngliche Sammlung nicht verändert, sondern eine neue Sammlung erstellt. Das Umwandeln z.B. einer Liste in ein Set ist auch eine gängige Methode, um Duplikate zu entfernen. :::: {.grid} ::: {.g-col-8} ```{python} alle_namen = ['Goku', 'Vegeta', 'Goku', 'Goku', 'Gohan', 'Vegeta'] einzigartige_namen = set(alle_namen) print(alle_namen) print(einzigartige_namen) ``` ::: ::: {.g-col-4} ```{python} x = {1, 2, 3} y = list(x) print(x) print(y) ``` ::: :::: ## Hinzufügen Anstellen von `append()` oder `insert()` wie bei Listen gibt es bei Sets die Methode `add()`. Diese fügt ein Element hinzu, falls es noch nicht im Set enthalten ist. Falls es bereits enthalten ist, passiert nichts. ```{python} x = {1, 2, 3} x.add(4) x ``` ## Entfernen Anstellen von `remove()` wie bei Listen gibt es bei Sets die Methoden `discard()` und `remove()`. Diese entfernt ein Element, falls es im Set enthalten ist. Falls es nicht enthalten ist, passiert nichts. Beide Methoden unterscheiden sich nur darin, dass `remove()` einen Fehler wirft, falls das Element nicht enthalten ist, während `discard()` dann einfach nichts tut. :::: {.grid} ::: {.g-col-6} ```{python} x = {1, 2, 3} x.discard(3) x ``` ::: ::: {.g-col-6} ```{python} x = {1, 2, 3} x.discard(4) x ``` ::: :::: :::: {.grid} ::: {.g-col-6} ```{python} x = {1, 2, 3} x.remove(3) x ``` ::: ::: {.g-col-6} ```{python} #| eval: False x = {1, 2, 3} x.remove(4) # ``` ```{python} #| echo: False x = {1, 2, 3} try: x.remove(4) except KeyError as e: print(f"Error: {e}") ``` ::: :::: Es gibt wie auch bei Listen die Methode `pop()`. Allerdings wird hier nicht wie bei Listen immer das letzten Element entfernt, sondern ein zufälliges. Das liegt daran, dass Sets ja nicht geordnet sind, sodass es sozusagen kein "letztes" Element gibt. Auch die Methode `clear()` funktioniert wie bei Listen und entfernt alle Elemente aus dem Set. ## Set-Operationen Sets haben auch spezielle Methoden, die Listen und Tuples nicht haben. Diese eignen sich speziell für Mengenoperationen von Daten ohne Duplikate. Set bedeutet im englischen ja auch ["Menge" im mathematischen Sinne](https://www.wikiwand.com/de/Menge_(Mathematik)). Mengenoperationen sind z.B. Vereinigung, Schnittmenge und Differenz und ihr Konzept wird beispielsweise bei [Venn-Diagrammen](https://www.wikiwand.com/de/Mengendiagramm) wie diesem hier angesetzt: <div style="text-align: center;"> ![](../img/vennfun.png){height=400} </div> Die wichtigsten Mengenoperationen werden hier kurz vorgestellt. Es sei darauf hingewiesen, dass hier immer nur mit zwei Sets (`x` und `y`) gearbeitet wird, aber die Methoden i.d.R. auch mit mehreren Sets funktionieren. ### Union (Vereinigung) :::: {.columns} ::: {.column width='80%'} Sets können vereinigt werden, d.h. es werden alle Elemente beider Sets in einem neuen Set zusammengefasst. Das geht entweder via `union()` oder `|`. ::: ::: {.column width='20%'} ![](../img/Venn0111.svg.png){width=200} ::: :::: :::: {.grid} ::: {.g-col-6} ```{python} x = {1, 2} y = {2, 3} z = x.union(y) print(x) print(y) print(z) ``` ::: ::: {.g-col-6} ```{python} x = {1, 2} y = {2, 3} z = x | y print(x) print(y) print(z) ``` ::: :::: Der Unterschied ist, dass `union()` auch andere Sammlungen (Listen, Tuples...) akzeptiert und automatisch in Sets umwandelt, während `|` nur Sets akzeptiert. ### Intersection (Schnittmenge) :::: {.columns} ::: {.column width='80%'} Sets können auch geschnitten werden, d.h. es werden nur die Elemente in einem neuen Set zusammengefasst, die in beiden Sets enthalten sind. Das geht entweder via `intersection()` oder `&`. ::: ::: {.column width='20%'} ![](../img/Venn0001.svg.png){width=200} ::: :::: :::: {.grid} ::: {.g-col-6} ```{python} x = {1, 2} y = {2, 3} z = x.intersection(y) print(x) print(y) print(z) ``` ::: ::: {.g-col-6} ```{python} x = {1, 2} y = {2, 3} z = x & y print(x) print(y) print(z) ``` ::: :::: Wieder ist der Unterschied, dass `intersection()` auch andere Sammlungen (Listen, Tuples...) akzeptiert und automatisch in Sets umwandelt, während `&` nur Sets akzeptiert. Oft reicht bereits die Information, ob es überhaupt Elemente in der Schnittmenge gibt, und nicht die Schnittmenge selbst. Für diesen Fall gibt es die Methode `isdisjoint()`, die `True` zurückgibt, falls **keine** Elemente in der Schnittmenge sind. :::: {.grid} ::: {.g-col-6} ```{python} x = {1, 2} y = {2, 3} x.isdisjoint(y) ``` ::: ::: {.g-col-6} ```{python} x = {1, 2} y = {3, 4} x.isdisjoint(y) ``` ::: :::: ### Difference :::: {.columns} ::: {.column width='80%'} Sets können auch voneinander abgezogen werden, d.h. es werden nur die Elemente in einem neuen Set zusammengefasst, die in einem Set enthalten sind, aber nicht im anderen. Das geht entweder via `difference()` oder `-`. ::: ::: {.column width='20%'} ![](../img/Venn0100.svg.png){width=200} ::: :::: :::: {.grid} ::: {.g-col-6} ```{python} x = {1, 2} y = {2, 3} z = x.difference(y) print(x) print(y) print(z) ``` ::: ::: {.g-col-6} ```{python} x = {1, 2} y = {2, 3} z = x - y print(x) print(y) print(z) ``` ::: :::: ### Symmetric Difference :::: {.columns} ::: {.column width='80%'} Sets können auch symmetrisch voneinander abgezogen werden, d.h. es werden nur die Elemente in einem neuen Set zusammengefasst, die in einem Set enthalten sind, aber nicht im anderen. Das geht entweder via `symmetric_difference()` oder `^`. ::: ::: {.column width='20%'} ![](../img/Venn0110.svg.png){width=200} ::: :::: :::: {.grid} ::: {.g-col-6} ```{python} x = {1, 2} y = {2, 3} z = x.symmetric_difference(y) print(x) print(y) print(z) ``` ::: ::: {.g-col-6} ```{python} x = {1, 2} y = {2, 3} z = x ^ y print(x) print(y) print(z) ``` ::: :::: ### Subset/Superset Schließlich kann es auch von Interesse sein zu prüfen ob ein Set ein Subset (Teilmenge) oder Superset (Obermenge) eines anderen Sets ist. Das geht entweder via `issubset()` oder `<`/`<=` bzw. `issuperset()` oder `>`/`>=`. :::: {.grid} ::: {.g-col-3} ```{python} x = {1} y = {1, 2} print(x.issubset(y)) print(x <= y) print(x < y) ``` ::: ::: {.g-col-3} ```{python} x = {1, 2} y = {1, 2} print(x.issubset(y)) print(x <= y) print(x < y) ``` ::: ::: {.g-col-3} ```{python} x = {1, 2} y = {1, 2} print(x.issuperset(y)) print(x >= y) print(x > y) ``` ::: ::: {.g-col-3} ```{python} x = {1, 2} y = {1} print(x.issuperset(y)) print(x >= y) print(x > y) ``` ::: :::: # Übungen ::: {.webex-check .webex-box} ```{r} #| echo: false #| results: asis q <- "Erzeuge dir folgende Liste: `liste = ['BMW', 'Audi', 'Mercedes', 'VW', 'Porsche', 'Audi', 'BMW']`. Nutze die Funktionalität von Sets, um die Liste durch Umwandlung in ein Set von Duplikaten zu befreien. Sorge danach dafür, dass das Ergebnis aber wieder in einer Liste (und nicht eine Set) vorliegt und alphabetisch sortiert ist." q_choices <- c(answer="Geschafft") cat(q,longmcq(q_choices)) ``` Prüfe ob bzw. welche der folgenden Tuples bzgl. ihrer einzigartigen Elemente Subsets der anderen sind: ```{python} #| eval: false #| # erzeuge einen Tupel mit 100 elementen, die zufällig aus 1 bis 1000 gewählt werden id_kunden_alle = ( 536, 731, 844, 226, 463, 60, 649, 242, 893, 364, 773, 509, 536, 548, 248, 104, 816, 479, 866, 67, 652, 695, 873, 247, 185, 46, 973, 537, 403, 109, 618, 491, 129, 450, 279, 701, 742, 615, 92, 672, 799, 90, 695, 99, 325, 618, 136, 26, 183, 761, 843, 788, 415, 655, 202, 203, 354, 411, 727, 131, 513, 120, 631, 202, 603, 312, 104, 635, 880, 823, 126, 471, 89, 278, 564, 215, 42, 889, 768, 155, 384, 555, 477, 122, 383, 965, 954, 360, 549, 560, 699, 935, 743, 585, 165, 421, 736, 908, 46, 17 ) id_kunden_positives_feedback = (247, 185, 46, 973, 537, 403, 109, 618, 491, 129, 450, 279, 701, 742, 615, 92, 672, 799, 90, 695, 99, 325, 618, 136, 26, 183, 761, 843, 788, 415, 655, 202, 203, 354, 411, 727, 131, 513, 120, 631, 202, 603, 312, 104, 635, 880, 823, 126, 471, 89, 278, 564, 215, 42, 889, 768, 155, 384, 555, 477, 122, 383, 965, 954, 360, 549, 560, 699, 935, 743, 585, 165, 421, 736, 247, 185, 46, 973, 537, 403, 247, 185, 46, 973, 537, 403, 247, 185, 46, 973, 537, 403, 247, 185, 46, 973, 537, 403, 247, 185, 46, 973, 537, 403 ) id_kunden_gekuendigt = (731, 743, 585) ``` ```{r} #| echo: false #| results: asis q_choices <- c(answer="Geschafft") cat(longmcq(q_choices)) ``` :::