import numpy as npNumPy Arrays
Nachdem wir die wichtigsten Grundlagen in Python kennengelernt haben, können wir uns nun mit dem ersten zusätzlichen Model beschäftigen: NumPy. NumPy steht für numerical python und ist eine Bibliothek, die das Rechnen mit Zahlen in Python erleichtert und auch beschleunigt. Es ist eine der wichtigsten Bibliotheken in Python und wird in fast jedem wissenschaftlichen Projekt verwendet.
Es sei an dieser Stelle vorweggenommen, dass NumPy 2005 veröffentlicht wurde, während Pandas 2008 veröffentlicht wurde. Pandas baut auf NumPy auf und ist im Grunde eine Erweiterung von NumPy. Aus diesem Grund beschäftigen wir uns hier zuerst also mit NumPy. Trotzdem werden wir erstmals Daten in Tabellen auswerten und auch importieren/exportieren, wenn wir uns mit Pandas beschäftigen.
Dass man np als Kürzel für NumPy verwendet, ist in der Python-Community so weit verbreitet ist, dass es schon komisch wäre, wenn man es anders handhabt:
Showcase: Einfacher & Schneller
Noch bevor die genaue Funktionsweise von NumPy erklärt wird, soll hier ein kleines Beispiel gezeigt werden, wie NumPy das Rechnen mit Zahlen erleichtert und beschleunigt. Zum Vergleich wollen wir folgendes einmal mit Listen und mit NumPy-Arrays tun: Für die Werte 1-5, welche in einem Objekt gespeichert sind, sollen die Quadratzahlen berechnet werden:
# Liste mit Loop
x = list(range(1, 6))
y = []
for i in x:
y.append(i**2)
print(x)
print(y)[1, 2, 3, 4, 5]
[1, 4, 9, 16, 25]# Liste mit List Comprehension
x = list(range(1, 6))
y = [i**2 for i in x]
print(x)
print(y)[1, 2, 3, 4, 5]
[1, 4, 9, 16, 25]# Array
x = np.arange(1, 6)
y = x**2
print(x)
print(y)[1 2 3 4 5]
[ 1 4 9 16 25]Es wird direkt offensichtlich, dass der Code mit NumPy deutlich kürzer ist. Das liegt daran, dass NumPy speziell für das Rechnen mit Zahlen geschrieben wurde und deshalb in diesem Fall die Quadrierung direkt auf das Array, also jede einzelne Zahl im Array, angewendet werden kann. Bei Listen ist das nicht ohne weiteres möglich - stattdessen müssen wir dort einen Loop verwenden, um jede Zahl in der Liste zu quadrieren. Dafür sind hier zwei verschiedene Varianten gezeigt: Einmal mit einem Loop und einmal mit einer List Comprehension (siehe Kapitel 2.5). Der NumPy-Ansatz ist aber kürzer als beide Varianten mit Listen.
Neben der Kürze des Codes ist auch die Geschwindigkeit ein wichtiger Vorteil von NumPy. Hier wird mittels dem timeit Modul die Zeit gemessen, die benötigt wird, um die Quadrate der Zahlen 1-1000 zu berechnen. Die Zeit wird dabei in Sekunden gemessen und das Ganze 1000 Mal wiederholt. Das Ergebnis ist, dass NumPy in diesem Fall etwa 100x schneller ist als Listen:
import timeit
code_liste = """
x = list(range(1, 1001))
y = [i**2 for i in x]
"""
liste_zeit = timeit.timeit(
stmt=code_liste,
number=1000,
globals=globals()
)
print(liste_zeit)0.07605289999992237#
code_array = """
x = np.arange(1, 1001)
y = x**2
"""
array_zeit = timeit.timeit(
stmt=code_array,
number=1000,
globals=globals()
)
print(array_zeit)0.0028911999997944804NumPy Arrays
Das wichtigste Objekt in NumPy ist das ndarray (kurz für n-dimensional array). Ein Array ist eine Datenstruktur, die es erlaubt, mehrere Werte in einer Variablen zu speichern. Ein ndarray kann also mehrere Werte speichern - so wie auch Listen, Tuples, Sets und Dictionaires. Im Gegensatz zu Listen, Tuples, Sets und Dictionaries in Python, die heterogen sein können (verschiedene Objekttypen speichern), sind ndarray-Objekte homogen. Das bedeutet, dass sie ausschließlich Werte eines einzigen Datentyps enthalten. Diese Homogenität ermöglicht es, dass die Daten zusammenhängend im Speicher abgelegt werden, was den Zugriff und die Verarbeitungsgeschwindigkeit erheblich verbessert. Darüber hinaus bietet NumPy viele numerische Funktionen an, die speziell für mit Zahlen gefüllte ndarray-Objekte entwickelt wurden, um die Arbeit mit numerischen Daten effizient und effektiv zu gestalten.
erzeugen
np.array()
Ein Array kann auf verschiedene Weisen erstellt werden. Die wohl intuitivste ist, ein Array aus einer Liste zu erstellen. Hier erzeugen wir erst eine Liste und konvertieren sie dann in ein array. Neben den Objekten selbst, lassen wir uns auch die Typen der Objekte mittels print(type(...)) ausgeben:
a = [1, 2, -3, 42] # Liste
b = np.array(a)print(a)
print(type(a))[1, 2, -3, 42]
<class 'list'>print(b)
print(type(b))[ 1 2 -3 42]
<class 'numpy.ndarray'>Neben Listen können auch Tuples in Arrays umgewandelt werden. Die übergebenen Listen und Tuples dürfen dabei sogar geschachtelt sein (also Listen in Listen, Tuples in Tuples, etc.) - dann werden aber auch mehrdimensionale Arrays erstellt (später mehr dazu).
a = (1, 2, -3, 42) # Tuple
b = np.array(a)
print(b)[ 1 2 -3 42]c = [(1, 2, 3), [4, 5, 6]] # Tuple & Liste in Liste
d = np.array(c)
print(d)
print(type(d))[[1 2 3]
[4 5 6]]
<class 'numpy.ndarray'>weitere Funktionen
Neben np.array() gibt es noch viele weitere Funktionen, um Arrays zu erstellen. Hier sollen einige davon vorgestellt werden:
np.zeros(3) # Array mit 3 Nullenarray([0., 0., 0.])np.ones(3) # Array mit 3 Einsenarray([1., 1., 1.])np.full(3, 4.) # Array mit 3 Vierenarray([4., 4., 4.])Die Funktionen np.zeros(), np.ones() erzeugen wie beschrieben Arrays mit Nullen und Einsen. Beim Ausgeben der Arrays sieht man außerdem, dass dort 0. anstatt 0 und 1. anstatt 1 steht. Das liegt daran, dass NumPy standardmäßig mit float-Zahlen und nicht int-Zahlen arbeitet (siehe Kapitel 2.2 Datentypen). Man kann es auch prüfen, indem man sich den type() eines einzelnen Elements des Arrays ausgeben lässt, z.B. via type(np.zeros(3)[0]). Aus diesem Grund - und um zwischen den Beispielen konsistent zu bleiben - haben wir auch in der Funktion np.full() eine float-Zahl 4. und nicht 4 übergeben.
Es ist auch leicht möglich sich Zufallszahlen ausgeben zu lassen. Hierbei gibt es verschiedene Funktionen, die Zufallszahlen generieren. Die Funktion np.random.rand() gibt z.B. Zufallszahlen zwischen 0 und 1 aus, wohingegen bei der Funktion np.random.randint() ganze Zufallszahlen zwischen zwei selbstgewählten Grenzen generiert werden.
np.random.rand(3)array([0.03415383, 0.98916642, 0.63240268])np.random.randint(low=10, high=20, size=3)array([16, 11, 18], dtype=int32)Schließlich seien noch np.arange und np.linspace genannt. Beide Funktionen generieren Zahlenfolgen. np.arange generiert dabei eine Zahlenfolge, die sich aus einer Start- und Endzahl und einem Schritt zusammensetzt. np.linspace generiert eine Zahlenfolge, die sich aus einer Start- und Endzahl und einer Anzahl an Zahlen zusammensetzt.
# Zahlen von 0 bis 10 in 2er Schritten
np.arange(0, 11, 2)array([ 0, 2, 4, 6, 8, 10])# 5 Zahlen zwischen 0 und 10
np.linspace(0, 10, 5)array([ 0. , 2.5, 5. , 7.5, 10. ])Es fällt auf, dass die beiden Funktionen sich unterschiedlich bzgl. des Einschluss des Endwerts verhalten. Bei np.arange() ist der Endwert nicht enthalten (wie auch bei range() oder beim Slicing von Listen, siehe Kapitel 2.3), bei np.linspace() hingegen schon. Außerdem produziert np.arange() standardmäßig Integer und np.linspace() Floats.
Mehrdimensional Arrays
Bisher wurden nur eindimensionale Arrays gezeigt und diese werden wir auch vorrangig brauchen. Es gibt aber auch mehrdimensionale Arrays. Eindimensionale Arrays werden auch als Vektoren bezeichnet, zweidimensionale Arrays als Matrizen und mehrdimensionale Arrays als Tensoren. Außerdem gibt es natürlich auch 0-dimensionale Arrays, also Arrays die nur ein Element/eine Zahl enthalten, welche als Skalare bezeichnet werden.
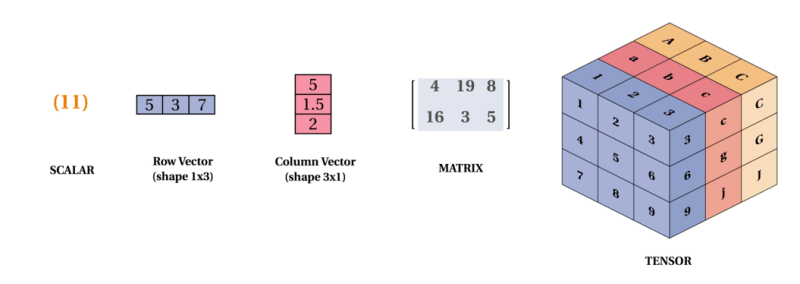
Quelle: Mukesh Mithrakumar
Wie oben kurz gezeigt, kann ein mehrdimensionales Array aus einer geschachtelten Liste oder einem geschachtelten Tuple erstellt werden. Ebenso, können aber auch Befehle wie np.reshape() verwendet werden, um aus einem eindimensionalen Array ein mehrdimensionales Array zu erstellen.
x = np.array([[1, 2], [3, 4]])
print(x)[[1 2]
[3 4]]x = np.array([1, 2, 3, 4, 5, 6])
y = np.reshape(x, (2, 3))
print(y)[[1 2 3]
[4 5 6]]x = np.array([1, 2, 3, 4, 5, 6])
y = np.reshape(x, (3, 2))
print(y)[[1 2]
[3 4]
[5 6]]Bis auf die unten angegebene weitere Ressource soll hier aber nicht weiter auf mehrdimensionale Arrays eingegangen werden. Es sei nur gesagt, dass die meisten Funktionen, die auf eindimensionalen Arrays angewendet werden können, auch auf mehrdimensionalen Arrays angewendet werden können. Bereiche in denen mehrdimensionale Arrays benötigt werden, sind z.B. Bildverarbeitung, neuronale Netze und Simulationen. Gleichzeitig sind Matrizen auch Grundlage für die Schätzung von z.B. Regressionsmodellen, welche wir nutzen werden um Daten zu analysieren. Allerdings werden wir dafür bereitgestellte Funktionen nutzen, sodass wir selbst nicht mit mehrdimensionalen Arrays arbeiten müssen.
Übungen
Finde selbstständig, also mithilfe der Python Dokumentation und/oder des Internets heraus mit welchem Befehl meinarray.??? (1) man die Anzahl der Elemente eines Arrays herausfinden kann, (2) man die Elemente in einem Array der Größe nach sortieren kann.
mein_array = np.array([1, 9, 5])Zeige Anzahl Elemente: mein_array. Sortiere Elemente: mein_array.