import numpy as np
import matplotlib.pyplot as plt
import seaborn as snsVarianz und Standardabweichung
Schließlich wollen wir uns noch mit der Varianz und Standardabweichung beschäftigen. Beides sind Maße für die Streuung der Werte und speziell die Standardabweichung sieht man häufig in Kombination mit dem Mittelwert, z.B. als “Mittelwert plus/minus Standardabweichung” und wir werden am Ende dieses Kapitels auch ein entsprechendes Diagramm erstellen.
Varianz
Die Varianz (engl. variance) gibt einfach ausgedrückt an wie sehr Werte variieren. Genauer gesagt ist sie definiert als das arithmetische Mittel der quadrierten Abweichungen vom Mittelwert. Das mag auf den ersten Blick etwas kompliziert klingen, es lohnt sich aber zumindest einmal hier die Formel zu sehen und zu verstehen. Im Alltag gibt es natürlich Funktionen wie np.var() die das für uns berechnen, aber es ist immer gut zu wissen was dahinter steckt - vor allem wenn unerwartete Ergebnisse auftauchen.
Die Varianz wird oft als mit \(\sigma^2\) bezeichnet und berechnet sich wie folgt:
\[\sigma^2 = \frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n} \]
Dabei ist \(\bar{x}\) der Mittelwert und \(x_i\) die einzelnen Werte. Das Summenzeichen \(\sum\) bedeutet, dass alles was rechts davon steht für jeden Wert von \(i=1\) bis \(n\) berechnet und dann aufaddiert wird.
Nehmen wir an wir haben die Werte 10, 12 und 14. Dann ist \(n=3\) mit den Werten \(x_1=10\), \(x_2=12\) und \(x_3=14\). Der Mittelwert ist \(\bar{x}=12\) und die Varianz berechnet sich wie folgt:
\[\sigma^2 = \frac{(10-12)^2 + (12-12)^2 + (14-12)^2}{3} = \frac{4 + 0 + 4}{3} = \frac{8}{3} \approx 2.67\]
Zum Vergleich hier die Berechnung mittels numpy für jeweils 3 Zahlen, die denselben Mittelwert haben, aber unterschiedlich stark streuen:
zahlen = np.array([10, 12, 14])
print(np.mean(zahlen))
print(np.var(zahlen))12.0
2.6666666666666665zahlen = np.array([9, 12, 15])
print(np.mean(zahlen))
print(np.var(zahlen))12.0
6.0In gewisser Hinsicht ist die Varianz also nur die durchschnittliche Abweichung vom Mittelwert. Wenn Werte stark variieren, dann sind die einzelnen Abweichungen groß und die Varianz ist entsprechend hoch. Da die einzelnen Abweichungen vom Mittelwert aber positiv oder negativ sein können, wird diese Abweichung erst quadriert und dann gemittelt. Das Quadrieren verhindert also, dass positive und negative Abweichungen sich beim Aufaddieren gegenseitig aufheben.
Das Quadrieren führt aber auch dazu, dass die Varianz in den Quadraten der Einheiten gemessen wird. Wenn wir also z.B. davon ausgehen die Werte 10, 12 und 14 von oben Angaben in Metern waren, dann ist die Varianz in Quadratmetern. Das ist nicht unbedingt intuitiv und deshalb wird oft die Standardabweichung verwendet, die einfach die Wurzel der Varianz ist und damit wieder in den ursprünglichen Einheiten gemessen wird.
Standardabweichung
Die Standardabweichung (engl. standard deviation) ist also einfach die Wurzel der Varianz und wird oft mit \(\sigma\) bezeichnet.
Die Standardabweichung (engl. standard deviation, SD, StdDev) darf nicht mit dem Standardfehler (engl. standard error, SE, StdErr) verwechselt werden.
Der Vorteil der Standardabweichung gegenüber der Varianz ist wie gesagt, dass sie wieder in den ursprünglichen Einheiten gemessen wird und damit intuitiver ist. Daher ist die Standardabweichung eins der gängigsten Streuungsmaße und wird oft in Kombination mit dem Mittelwert verwendet.
Für folgende drei Beispielzahlen steht das Ergebnis unter den Code-Chunks auch in der typischen Schreibweise MW \(\pm\) StdAbw.
zahlen = [10, 12, 14]
print(np.mean(zahlen))
print(np.var(zahlen))
print(np.std(zahlen))12.0
2.6666666666666665
1.632993161855452\(12.0 \pm 1.6\)
zahlen = [9, 12, 15]
print(np.mean(zahlen))
print(np.var(zahlen))
print(np.std(zahlen))12.0
6.0
2.449489742783178\(12.0 \pm 2.4\)
zahlen = [9, 10, 12, 14, 15]
print(np.mean(zahlen))
print(np.var(zahlen))
print(np.std(zahlen))12.0
5.2
2.280350850198276\(12.0 \pm 2.3\)
Visualisierung
Zum Abschluss wollen wir noch ein Diagramm erstellen, das den Mittelwert und die Standardabweichung zeigt. Wir können wieder auf Personen B und E aus den vorherigen Kapiteln zurückgreifen.
noten_B = np.array([2, 3, 3, 2, 2, 2, 3, 2])
mw_B = np.mean(noten_B)
stdabw_B = np.std(noten_B)
print(mw_B)
print(stdabw_B)2.375
0.4841229182759271noten_E = np.array([2, 3, 4, 2, 1, 2, 3, 6])
mw_E = np.mean(noten_E)
stdabw_E = np.std(noten_E)
print(mw_E)
print(stdabw_E)2.875
1.4523687548277813Balkendiagramm mit Fehlerbalken
Eigentlich würde es Sinn ergeben unsere Abbildungen aus dem vorangegangenen Kapitel, die bereits Dot-Plots, Box-Plots und Mittelwerte enthalten, um die Standardabweichung zu erweitern. Das werden wir auch gleich tun, aber zuerst wollen wir uns die wohl typischste Visualisierung für Mittelwert und Standardabweichung ansehen: das Balkendiagramm mit Fehlerbalken (engl. Error bar).
Diese Dinge sind im folgenden Code neu:
-
plt.bar()erzeugt ein Balkendiagramm.- Mit
x=geben wir die Position des Balkens auf der x-Achse an, wobei wir erstmal wieder einen pseudo Wert0angeben, den wir daraufhin wieder mitplt.xticks([])verbergen. Eigentlich haben Balkendiagramme mehrere Balken, sodass die x-Achse dann auch Informationen enthält. Dazu kommen wir später. - Mit
height=muss die Höhe des Balkens angegeben werden. Oft ist das wie jetzt hier der Mittelwert. - Mit
yerr=kann zusätzlich die Länge eines Fehlerbalkens (in beide Richtungen) angegeben werden. Das ist hier die Standardabweichung. - Hier haben wir außerdem
capsize=10angegeben. Das betrifft die kleinen Striche an den Enden der Fehlerbalken. Standardmäßig - also wenn wir kein Argumentcapsizeangeben - ist der Wert 0, sodass die Striche nicht vorhanden und die Fehlerbalken somit nur vertikale Linien sind. Die Wahl zwischen diesen Optionen ist Geschmackssache.
- Mit
- In
plt.ylabel()nutzen wir mit\u00B1erstmals einen sogenannten Unicode-String.- Unicode ist ein internationaler Standard, der allen möglichen Zeichen, die in der Welt verwendet werden, einen Code zuweist. Der Unicode für das Plus/Minus-Zeichen ist
00B1(siehe z.B. hier). Wie man in der erzeugten Abbildung sieht, versteht Python bzw. Matplotlib Unicode und wir können es in Strings verwenden, indem wir es mit\ugefolgt von dem Code in den String schreiben.
- Unicode ist ein internationaler Standard, der allen möglichen Zeichen, die in der Welt verwendet werden, einen Code zuweist. Der Unicode für das Plus/Minus-Zeichen ist
plt.figure()
plt.title('Person B')
plt.bar(
x=0,
height=mw_B,
yerr=stdabw_B,
color='orange',
capsize=10
)
plt.ylabel('Noten (MW \u00B1 StdAbw)')
plt.ylim(0, 6)
plt.xticks([])
plt.show()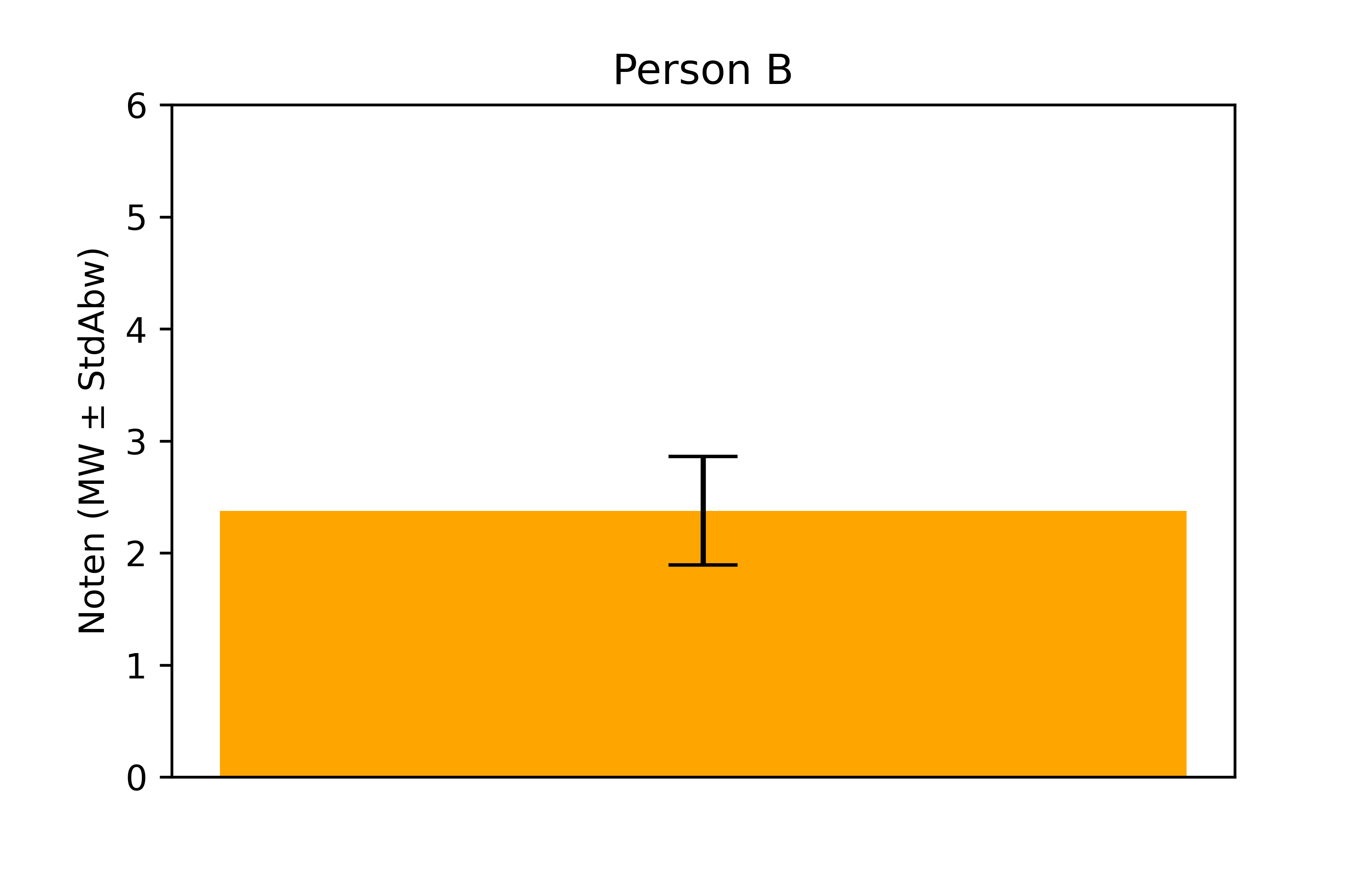
plt.figure()
plt.title('Person E')
plt.bar(
x=0,
height=mw_E,
yerr=stdabw_E,
color='firebrick',
capsize=10
)
plt.ylabel('Noten (MW \u00B1 StdAbw)')
plt.ylim(0, 6)
plt.xticks([])
plt.show()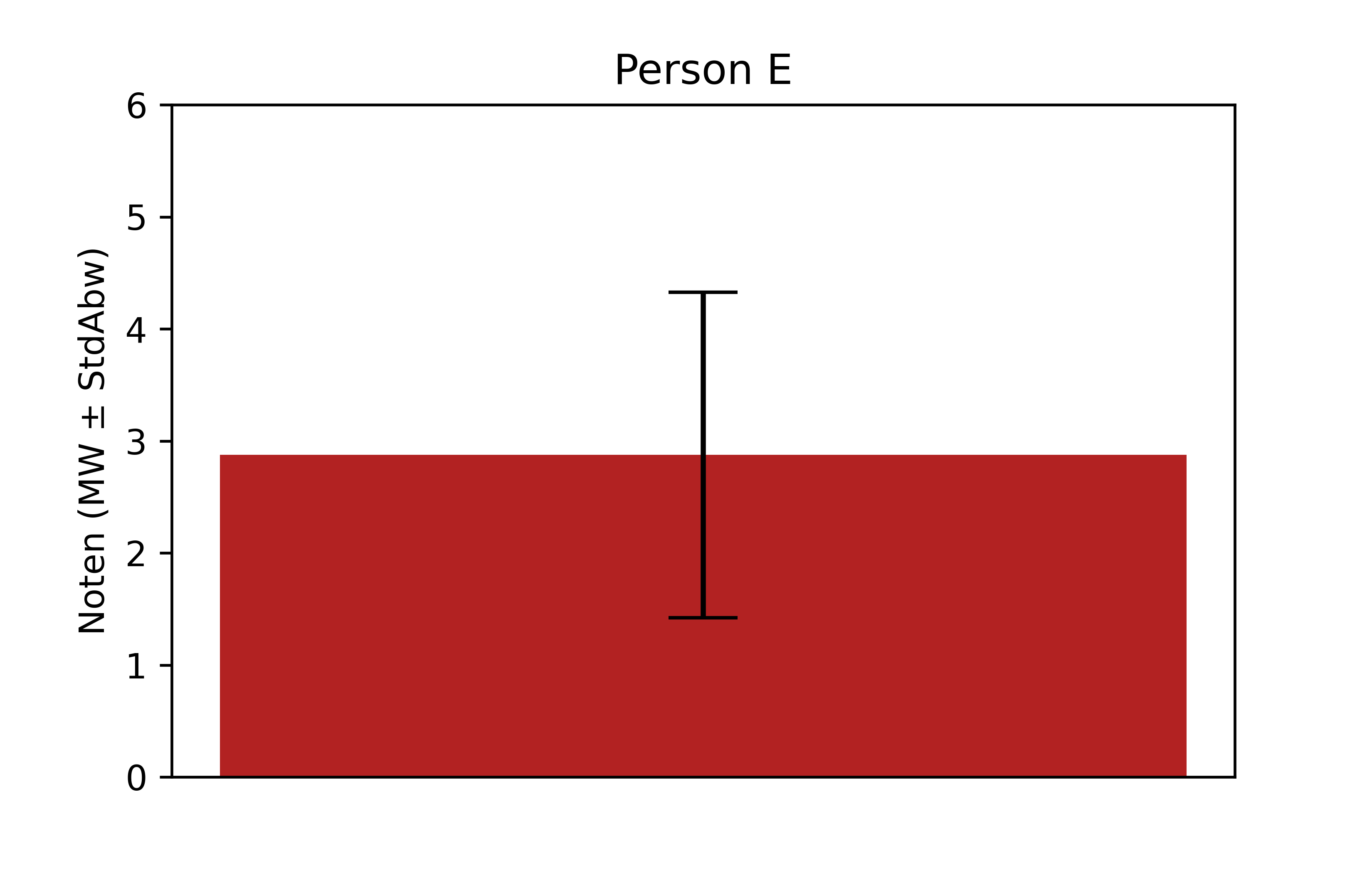
Diese Art Balkendiagramm mit Fehlerbalken ist sehr gängig und wird oft in wissenschaftlichen Veröffentlichungen verwendet. Natürlich ist sie nicht ohne Grund so beliebt, denn sie zeigt anschaulich den Mittelwert und die Streuung der Werte.
Was leider oft vernachlässigt wird, ist in der Abbildung anzugeben was die Balken und Fehlerbalken genau bedeuten. Dass der Balken den Mittelwert repräsentiert, ist meistens klar, aber was genau die Fehlerbalken darstellen, ist oft nicht ersichtlich. Tatsächlich ist es nämlich nicht so, dass die Fehlerbalken immer die Standardabweichung darstellen. Stattdessen können sie z.B. auch den Standardfehler oder ein Vertrauensintervall darstellen (beides besprechen wir später). An dieser Stelle könnte man auch argumentieren, dass die Bezeichnung “Fehlerbalken” an sich irreführend ist, da sie ja nicht unbedingt den (Standard)Fehler, sondern viel mehr irgendeine Art Streuung/Präzision darstellen. Es könnte prinzipiell auch sein, dass die Fehlerbalken den Interquartilsabstand darstellen. Nichts davon ist per se falsch oder zu bevorzugen, aber es muss unbedingt den lesenden Personen klar gemacht werden, welches Streuungsmaß sie vor sich haben.
Fehlerbalken sind von diesem Problem häufig betroffen, aber die Botschaft gilt natürlich prinzipiell für alles was in einer Abbildung dargestellt wird. Man sollte sich immer fragen ob alle Informationen ersichtlich sind. Am besten fragt man sich ob eine Person, die die Daten und Auswertung nicht kennt, die Abbildung verstehen würde. Man selbst steht ja nicht immer zur Verfügung um zu erklären oder Rückfragen zu beantworten.
Alternative zu Balkendiagramm
Nun haben wir also den gängigen Weg gesehen, den Mittelwert und die Standardabweichung als Balkendiagramm mit Fehlerbalken zu visualisieren. Doch wie so oft gibt es auch hier Kritik. Zuerst sollten wir nochmal einen Schritt zurück gehen und uns klar machen, dass dies zwar eine andere Art Abbildung ist, wir ja aber weiterhin dieselben Noten darstellen. Zum Vergleich hier nochmal für Person E die Abbildung aus dem letzten und diesem Kapitel nebeneinander:
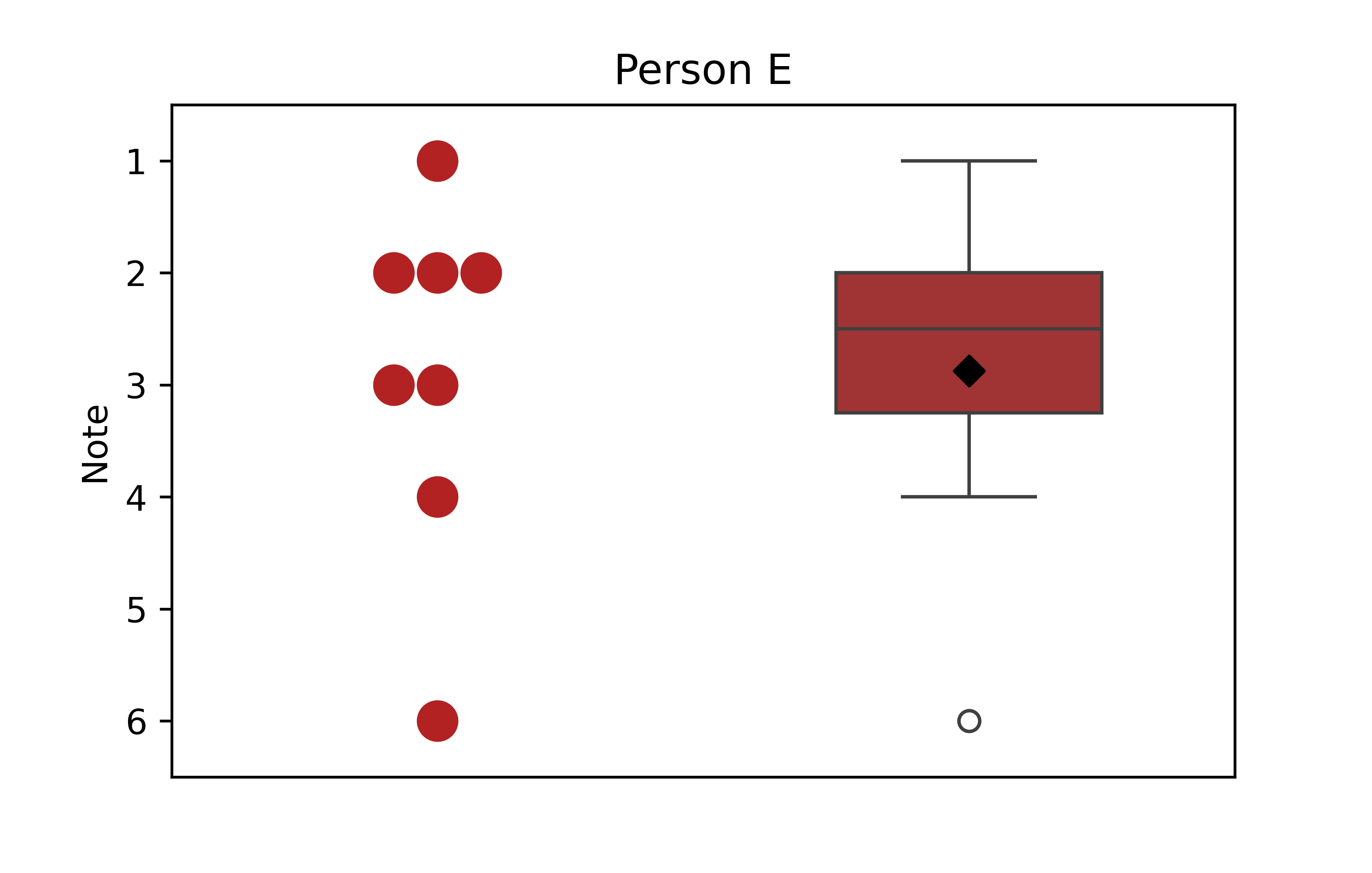
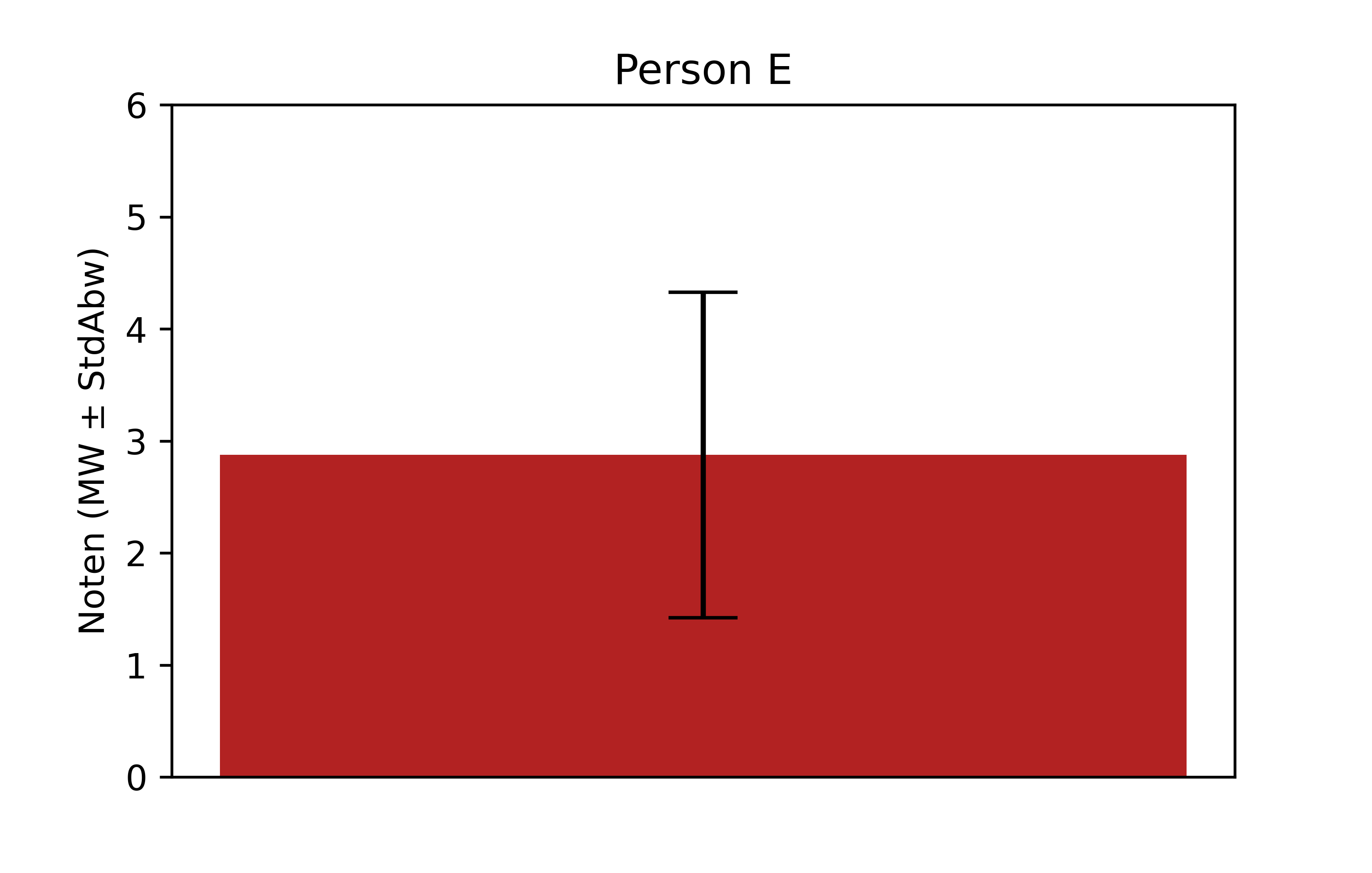
Wenn wir die beiden Abbildungen vergleichen fällt auf, dass deutlich mehr Informationen in der ersten Abbildung stecken. Umgekehrt fehlt nur die Standardabweichung in der linken Abbildung, da die Höhe des Balkens rechts ja links als Raute abgebildet ist. Stellt man sich vor, dass man zwei Personen jeweils nur eine der beiden Abbildungen zeigt und sie dann fragt was sie über die Daten sagen können, dann dürften die Antworten sehr unterschiedlich ausfallen. Hier eine tabellarische Gegenüberstellung welche Informationen in welcher Abbildung enthalten sind:
’| Information | Abbildung links | Abbildung rechts |
|---|---|---|
| Mittelwert | ja | ja |
| Standardabweichung | - | ja |
| Median | ja | - |
| Modus | ja | - |
| Spannweite / Min. / Max. | ja | - |
| Interquartilsabstand / Q1 / Q3 | ja | - |
| Anzahl Werte | ja | - |
| Verteilung Werte | ja | - |
| Alle Werte | ja | - |
| Ausreißer | ja | - |
’
Diese Kritik an den klassischen Balkendiagrammen mit Fehlerbalken ist nicht neu und wird von Experten der Datenvisualisierung regelmäßig geäußert. Die Balkendiagramme mit Fehlerbalken werden in dem Zuge aufgrund der Ähnlichkeit zu Dynamitstangen auch etwas abfällig als “Dynamite Plots” bezeichnet. Eine ausführliche Diskussion dazu findet sich in den weiteren Ressourcen (unten). Es gibt auch Memes zum Thema:


Quelle beide: Cédric Scherer
Die Alternative, die in den Memes und auch in der Diskussion um die “Dynamite Plots” vorgeschlagen wird, ist der sogenannte Raincloud-Plot (aufgrund der Ähnlichkeit mit einer Regenwolke). Das ist eine Kombination aus Punktediagramm, Box-Plot und Violin-Plot und zeigt ebenfalls alle Informationen, die in der Tabelle oben aufgeführt sind. Zwar haben wir in unserer linken Abbildung keinen Violin-Plot, dafür sind unsere Punkte als Dot-Plot dargestellt, was ebenfalls die Verteilung der Werte zeigt. Letztendlich sind Balkendiagramme (mit Fehlerbalken) weiterhin eine legitime Art Daten zu visualisieren, aber als Data Analyst ist es wichtig sich bewusst zu sein, dass sie vergleichsweise wenig Informationen enthalten. Die Entscheidung für eine bestimmte Art Abbildung hängt am Ende immer von den Daten und der Zielgruppe ab.
Als letzten Schritt in diesem Kapitel könnten wir nun noch versuchen selbst die Standardabweichung in unsere linke Abbildung einzuführen, da es die einzige Kennzahl aus der Vergleichstabelle ist, die dort noch fehlt. Prinzipiell müssten wir lediglich den Fehlerbalken an die Raute statt an den Balken anbringen. Statt aber zum dem Befehl, der die Raute zeichnet noch einen Befehl hinzuzufügen, der den Fehlerbalken zeichnet, würden wir hier plt.scatter() komplett ersetzen durch plt.errorbar(). Letzterer kann nämlich direkt Punkte/Raute und Fehlerbalken zeichnen. Schließlich sollten wir die Raute samt Fehlerbalken auch noch verschieben, da die Raute alleine zwar auf dem Box-Plot noch gut aussah, aber zusammen mit dem Fehlerbalken zu viel überlagert. Wir fügen also folgenden Code ein:
-
plt.errorbar()anstelle vonplt.scatter():-
x=0.5, sodass es zwischen unseren pseudo-x-Werten 0 (für den Dot-Plot) und 1 (für den Box-Plot) liegt. Damit wird auchzorderfür diesen Plot überflüssig. -
y=np.mean(noten_E), also den Mittelwert als Punkt. -
yerr=np.std(noten_E), also die Standardabweichung als Fehlerbalken. -
fmt='D', also die Raute als Marker. -
color='black', also die Farbe schwarz. -
capsize=5, also die Länge der Striche an den Enden des Fehlerbalkens.
-
-
plt.suptitle()undplt.title()um neben Titel auch etwas Erläuterung hinzuzufügen.
Achtung! Es kann sein, dass die bei euch erzeugte Abbildung nicht genau so aussieht wie die hier obwohl ihr den exakt gleichen Code verwendet. Das liegt wahrscheinlich daran, dass ihr eure seaborn Version aktualisieren müsst. Mehr dazu im folgenden Kapitel ‘4.A Module installieren’.
noten_E = np.array([2, 3, 4, 2, 1, 2, 3, 6])
pseudo_x = np.zeros(len(noten_E))
plt.figure()
plt.suptitle('Person E')
plt.title('Die Raute mit Fehlerbalken zeigt den Mittelwert und die Standardabweichung', fontsize=7)
sns.swarmplot(
x=pseudo_x,
y=noten_E,
color='firebrick',
size=12
)
sns.boxplot(
x=pseudo_x+1,
y=noten_E,
color='firebrick',
width=0.5
)
plt.errorbar(
x=0.5,
y=np.mean(noten_E),
yerr=np.std(noten_E),
fmt='D',
color='black',
capsize=5)
plt.yticks(np.arange(1, 7))
plt.ylim(6.5, 0.5)
plt.ylabel('Note')
plt.xlim(-0.5, 1.5)
plt.xticks([])
plt.show()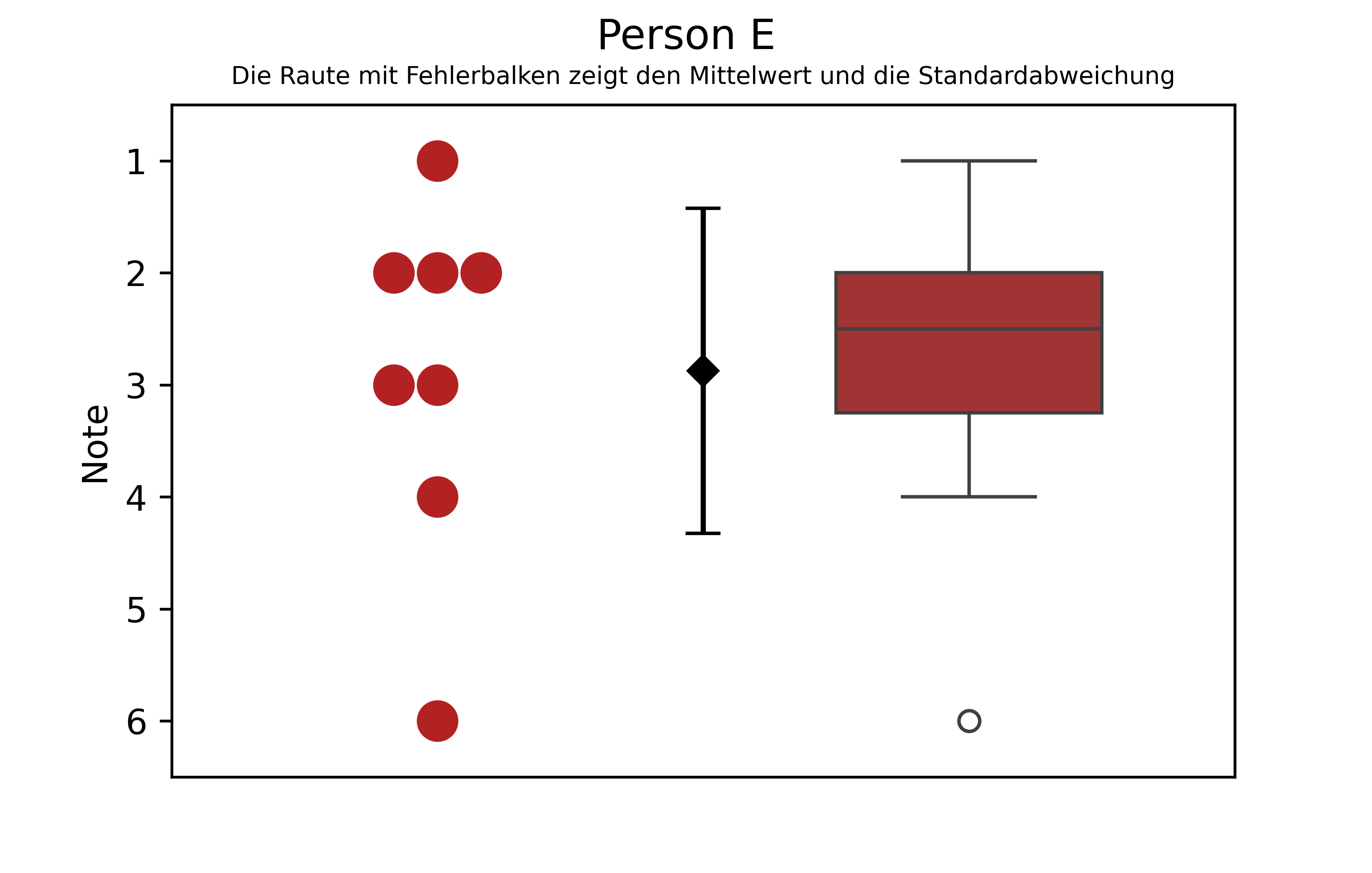
- Streuungsmaße [nur bis zur Überschrift “Streuungsmaße mit DATAtab berechnen”]
- Varianz und Standardabweichung in der Statistik (einfach erklärt)
- Statistik: Standardabweichung oder Standardfehler nach Gusto?
- Standard Error of the Mean vs. Standard Deviation: What’s the Difference?
- Visualizing Distributions with Raincloud Plots [Hier wird R-Code statt Python-Code gezeigt - dieser kann dementsprechend ignoriert werden. Es geht also nur darum den roten Faden des Blog Posts zu verstehen.]