import numpy as np
import matplotlib.pyplot as plt
import seaborn as snsMinimum, Maximum, Quantile, Quartile, Spannweite, Interquartilabstand
In diesem Kapitel wollen wir uns mit den Begriffen Minimum, Maximum, Quartile, Quantile, Spannweite und Interquartilsabstand (IQA) beschäftigen. Am bekanntesten sind wohl das Minimum als kleinster Wert und das Maximum als größter Wert in einer Datenmenge. Tatsächlich basieren aber alle diese Begriffe und auch der Median auf Quantilen.
Quantile
Ein Quantil (auch: \(p\)-Quantil, Empirisches Quantil, Stichprobenquantil) ist eine Kennzahl einer Datenmenge. Für jede Zahl \(p\) zwischen 0 und 1 teilt - vereinfacht dargestellt - ein \(p\)-Quantil die Daten so, dass ein Anteil der Daten von \(p\) kleiner als das \(p\)-Quantil ist und ein Anteil von \(1-p\) größer als das \(p\)-Quantil ist:
- Das 0-Quantil ist das Minimum der Datenmenge, da 0% (\(p\)) der Daten kleiner und 100% (\(1-p\)) der Daten größer als das 0-Quantil sind.
- Das 1-Quantil ist das Maximum der Datenmenge, da 100% (\(p\)) der Daten kleiner und 0% (\(1-p\)) der Daten größer als das 1-Quantil sind.
Die wohl nächstbekannten Quantile sind die Quartile. Sie heißen Quartile, da sie die Daten in vier Teile teilen:
- Das 0,25-Quantil ist das 1. Quartil (Q1, unteres Quartil), da 25% (\(p\)) der Daten kleiner und 75% (\(1-p\)) der Daten größer als das 0,25-Quantil sind.
- Das 0,5-Quantil ist der Median, da 50% (\(p\)) der Daten kleiner und 50% (\(1-p\)) der Daten größer als das 0,5-Quantil sind.
- Das 0,75-Quantil ist das 3. Quartil (Q3, oberes Quartil), da 75% (\(p\)) der Daten kleiner und 25% (\(1-p\)) der Daten größer als das 0,75-Quantil sind.
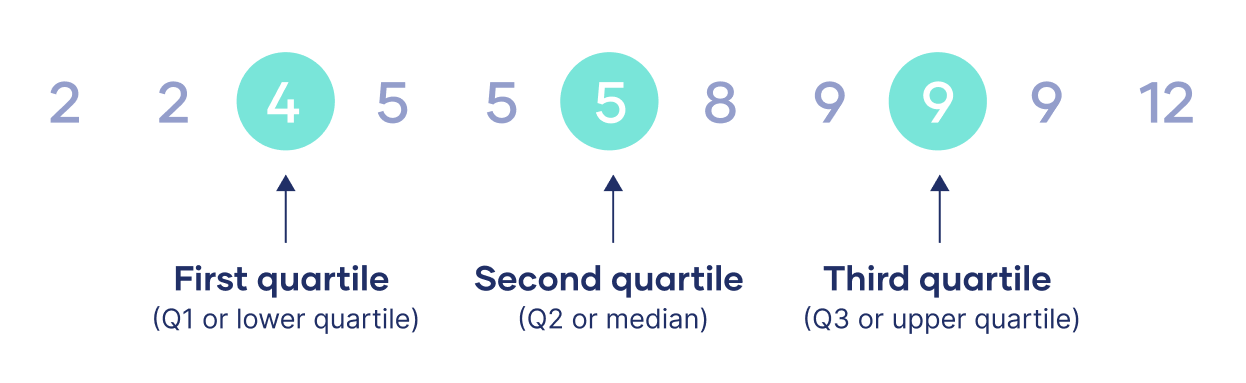
Quelle: Shaun Tuerny
Darüber hinaus können prinzipiell alle möglichen Quantile berechnet werden. So gibt es auch das 0,1-Quantil, das 0,9-Quantil, das 0,99-Quantil, das 0,01-Quantil, das 0,999-Quantil, das 0,001-Quantil, usw. Einige der Quantile tragen dann auch entsprechende Eigennamen, wie z.B. Terzile1, Quintile2, Dezile3 und die Perzentile4.
Man kann also sagen, dass einige Quantile häufiger als andere Quantile verwendet werden, aber prinzipiell kann jedes Quantil berechnet werden.
Spannweite und IQA
Ebenfalls auf den Quantilen basieren die Spannweite und der Interquartilsabstand (IQA). Nachdem wir bis hier nur Lagemaße genutzt haben sind diese beiden Kennzahlen also die ersten Streuuungsmaße auf die wir in diesem Kapitel eingehen.
Die Spannweite ist die Differenz zwischen dem Maximum und dem Minimum einer Datenmenge. Sie gibt also an, wie weit die Daten auseinander liegen. Die Spannweite ist ein einfaches Maß für die Streuung der Daten, aber sie ist auch sehr anfällig gegenüber Ausreißern.
Der Interquartilsabstand (IQA) (engl. interquartile range (IQR)) ist die Differenz zwischen dem 3. Quartil und dem 1. Quartil einer Datenmenge. Er gibt also an, wie weit die mittleren 50% der Daten auseinander liegen. Der IQA ist ein robustes Maß für die Streuung der Daten, da er nicht von einzelnen Ausreißern beeinflusst wird.
Wir ziehen die Noten von Personen B und E heran, um die Spannweite und den IQA zu berechnen und darzustellen.
noten_B = np.array([2, 3, 3, 2, 2, 2, 3, 2])
min_B = np.min(noten_B)
Q1_B = np.quantile(noten_B, 0.25)
Q3_B = np.quantile(noten_B, 0.75)
max_B = np.max(noten_B)
spannweite_B = max_B - min_B
IQA_B = Q3_B - Q1_B
print(Q1_B)
print(Q3_B)2.0
3.0print(spannweite_B)
print(IQA_B)1
1.0noten_E = np.array([2, 3, 4, 2, 1, 2, 3, 6])
min_E = np.min(noten_E)
Q1_E = np.quantile(noten_E, 0.25)
Q3_E = np.quantile(noten_E, 0.75)
max_E = np.max(noten_E)
spannweite_E = max_E - min_E
IQA_E = Q3_E - Q1_E
print(Q1_E)
print(Q3_E)2.0
3.25print(spannweite_E)
print(IQA_E)5
1.25Dabei fällt auf, dass es im Gegensatz zu np.min(), np.median() und np.max() keine Funktionen np.q1() und np.q3() gibt. Stattdessen nutzen wir np.quantile(), also die allgemeine Funktion zur Berechnung von Quantilen, und geben als zweites Argument den gewünschten Quantilwert an. Auch die Spannweite und der IQA berechnen wir selbst, indem wir die entsprechenden Werte voneinander abziehen, da es dafür keine Funktionen gibt.
Wir könnten nun überlegen wie man diese Quantile bzw. die daraus abgeleiteten Streuungsmaße visualisieren kann. Eine Möglichkeit wäre jeweils eine Linie für die Spannweite und das IQA einzuzeichnen. Das geht, indem wir die Funktion plt.vlines() nutzen, die vertikale Linien (wieder bei unserem pseudo x 0) zeichnet mit Start- (ymin=) und Endpunkt (ymax=) zeichnet. Wir nutzen sie also zweimal, um die Spannweite und den IQA einzuzeichnen. Dabei stellen wir sicher, dass die Linien unterschiedlich aussehen, indem wir die Farbe (colors=), Dicke (lw=, linewidth) und den Linienstil (linestyle=) anpassen.
pseudo_x = np.zeros(len(noten_B))plt.figure()
plt.title('Person B')
sns.swarmplot(
x=pseudo_x,
y=noten_B,
color='orange',
size=12
)
plt.vlines(
x=0,
ymin=min_B,
ymax=max_B,
colors='teal',
lw=6
)
plt.vlines(
x=0,
ymin=Q3_B,
ymax=Q1_B,
colors='cyan',
lw=3,
linestyle='dotted'
)
plt.yticks(np.arange(1, 7))
plt.ylim(6.5, 0.5)
plt.ylabel('Note')
plt.xticks([])
plt.show()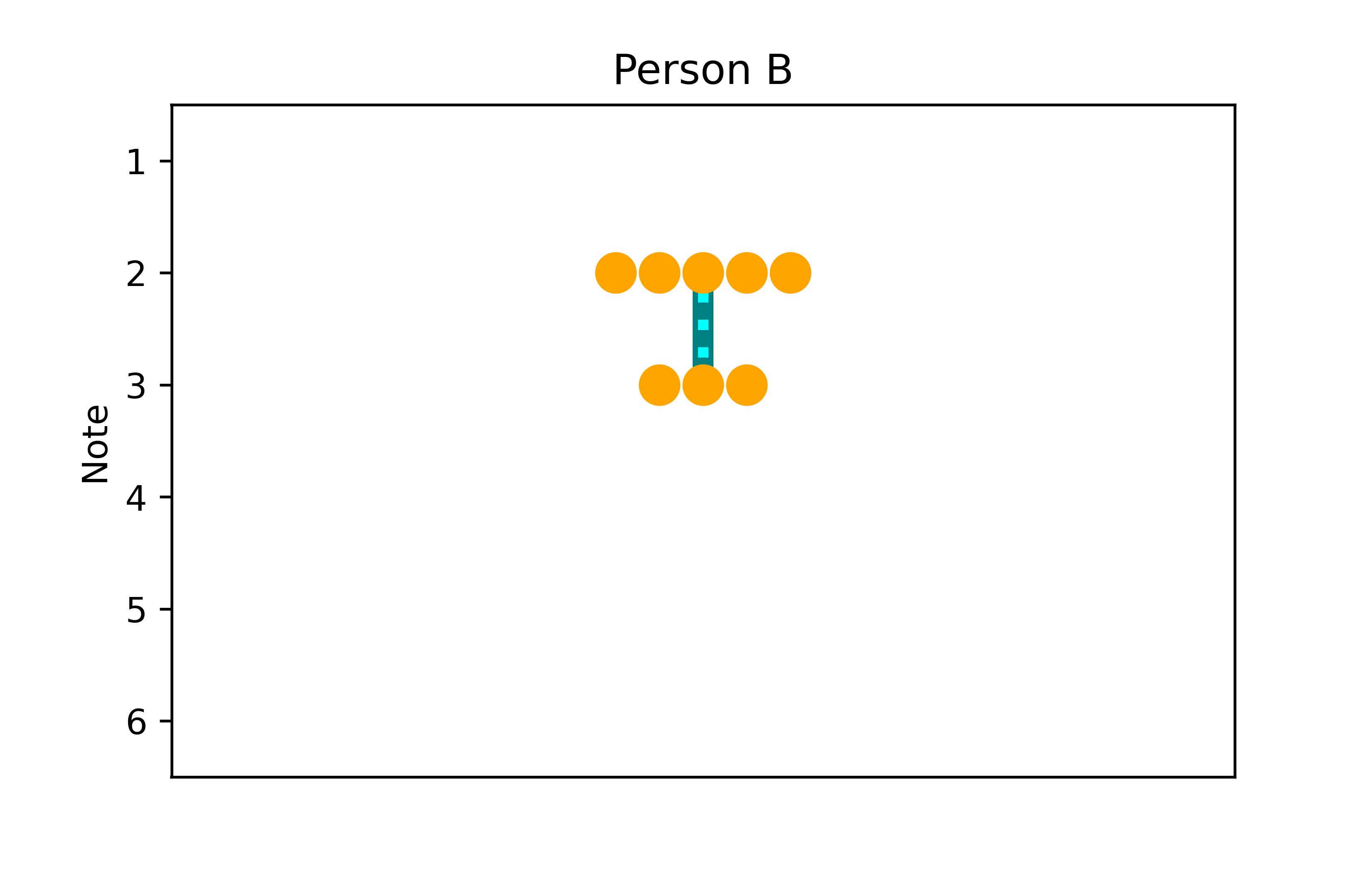
plt.figure()
plt.title('Person E')
sns.swarmplot(
x=pseudo_x,
y=noten_E,
color='firebrick',
size=12
)
plt.vlines(
x=0,
ymin=min_E,
ymax=max_E,
colors='teal',
lw=6
)
plt.vlines(
x=0,
ymin=Q3_E,
ymax=Q1_E,
colors='cyan',
lw=3,
linestyle='dotted'
)
plt.yticks(np.arange(1, 7))
plt.ylim(6.5, 0.5)
plt.ylabel('Note')
plt.xticks([])
plt.show()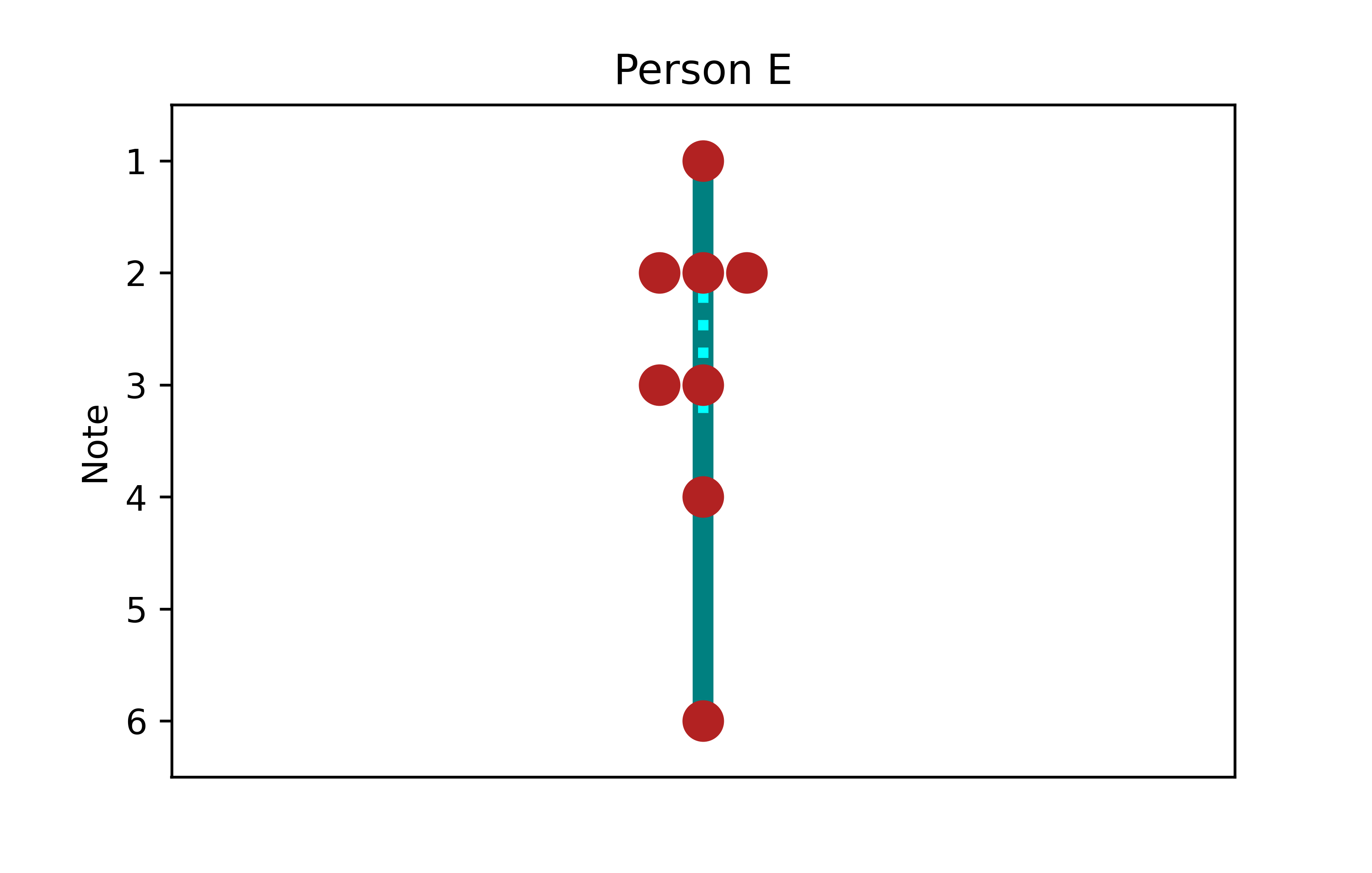
Box-Plots
Das hat also mehr oder weniger gut funktioniert - wir haben die Spannweite und den IQA visualisiert. Allerdings gibt es eine etablierte, bessere Möglichkeit, die Spannweite und den IQA zu visualisieren: Box-Plots.
Ein Box-Plot (auch: Box-Whisker-Plot, Kastengrafik) zeigt die Spannweite (also Minimum und Maximum) als eine Box/Kasten, den IQA (also oberes und unteres Quartil) als Whisker/Antenne, sowie den Median als Strich innerhalb der Box. Ein Box-Plot ist also eine kompakte und informative Darstellung einiger der wichtigsten Kennzahlen einer Datenmenge. In der Regel wird auch ermittelt, ob es Ausreißer gibt und diese dann als einzelne Punkte außerhalb der Whiskey dargestellt, obwohl die Whisker ja eigentlich die gesamte Spannweite der Daten abdecken. Wie einzelne Datenpunkte als Ausreißer identifiziert werden, ist allerdings nicht einheitlich geregelt. Die gängigste Methode ist die 1,5-IQA-Regel. Demnach sind alle Datenpunkte, die mehr als 1,5 mal den IQA von den Quartilen entfernt sind, Ausreißer.
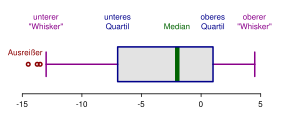
Box-Plot Beispiel 1. Quelle: Wikipedia
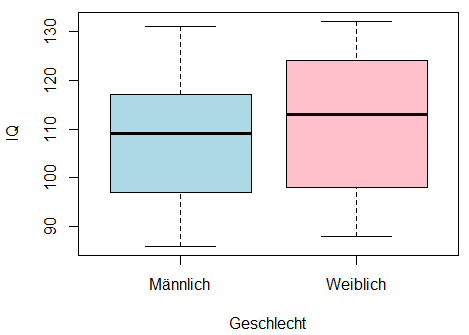
Box-Plot Beispiel 2. Quelle: Björn Walther
Wir können die Funktion sns.boxplot() nutzen, um Box-Plots zu erstellen. Die Funktion berechnet dann automatisch die Spannweite, den IQA und den Median und zeichnet sie in den Box-Plot ein.
plt.figure()
plt.title('Person B')
sns.swarmplot(
x=pseudo_x,
y=noten_B,
color='orange',
size=12
)
sns.boxplot(
x=pseudo_x,
y=noten_B
)
plt.yticks(np.arange(1, 7))
plt.ylim(6.5, 0.5)
plt.ylabel('Note')
plt.xticks([])
plt.show()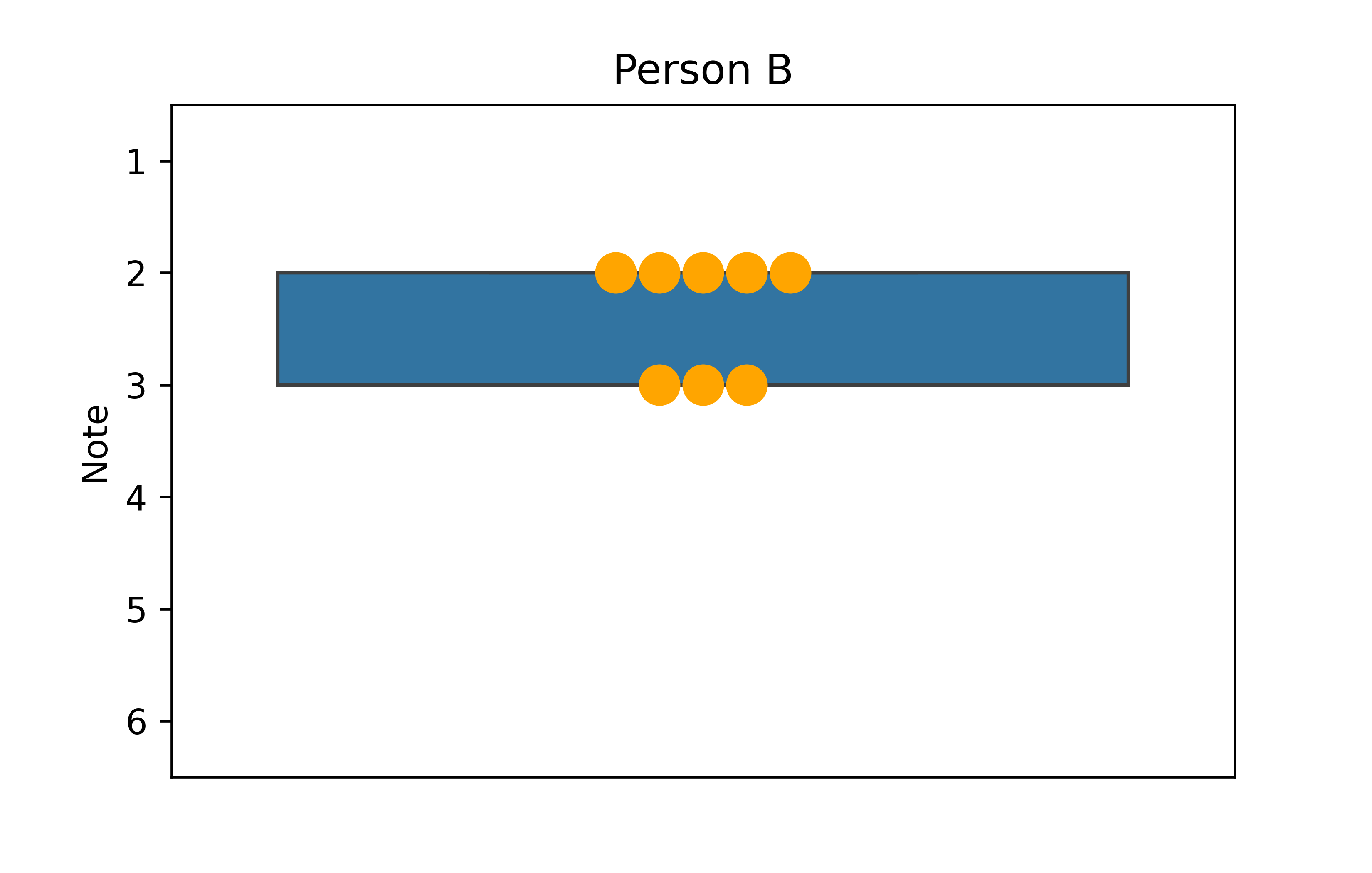
plt.figure()
plt.title('Person E')
sns.swarmplot(
x=pseudo_x,
y=noten_E,
color='firebrick',
size=12
)
sns.boxplot(
x=pseudo_x,
y=noten_E
)
plt.yticks(np.arange(1, 7))
plt.ylim(6.5, 0.5)
plt.ylabel('Note')
plt.xticks([])
plt.show()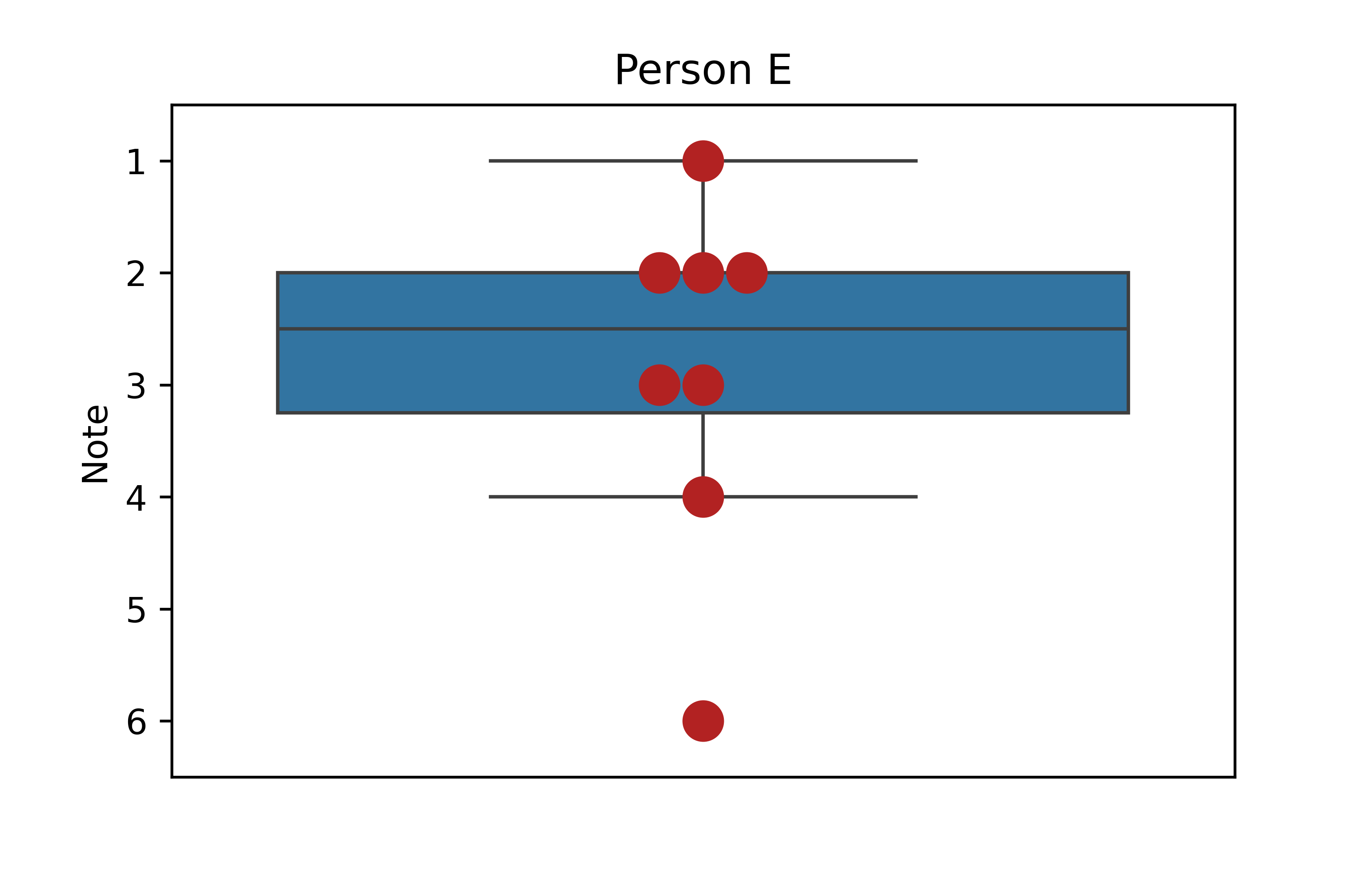
Es ist wohl auch Geschmackssache, aber diese Abbildung kann meines Erachtens verbessert werden, indem die Box-Plots neben die Punkte gezeichnet werden. Das geht z.B., indem wir die x-Werte der Box-Plots verschieben. Unsere Punkte werden ja weiterhin bei unserem pseudo x 0 eingezeichnet. Die Box-Plots können wir also z.B. bei pseudo_x+1, also 1 einzeichnen. Somit werden die Punkte bei x=0 und die Box-Plots bei x=1 eingezeichnet. Um die Skalierung (also quasi den Zoom) der x-Achse selbst anzupassen, nutzen wir dann auch plt.xlim(-0.5, 1.5). Außerdem passen wir noch die Farbe an und reduzieren die Breite der Box-Plots, damit sie nicht zu breit werden.
Achtung! Es kann sein, dass die bei euch erzeugten Abbildungen nicht genau so aussehen wie die hier obwohl ihr den exakt gleichen Code verwendet. Das liegt wahrscheinlich daran, dass ihr eure seaborn Version aktualisieren müsst. Mehr dazu im folgenden Kapitel ‘4.A Module installieren’.
plt.figure()
plt.title('Person B')
sns.swarmplot(
x=pseudo_x,
y=noten_B,
color='orange',
size=12
)
sns.boxplot(
x=pseudo_x+1,
y=noten_B,
color='orange',
width=0.5
)
plt.yticks(np.arange(1, 7))
plt.ylim(6.5, 0.5)
plt.ylabel('Note')
plt.xlim(-0.5, 1.5)
plt.xticks([])
plt.show()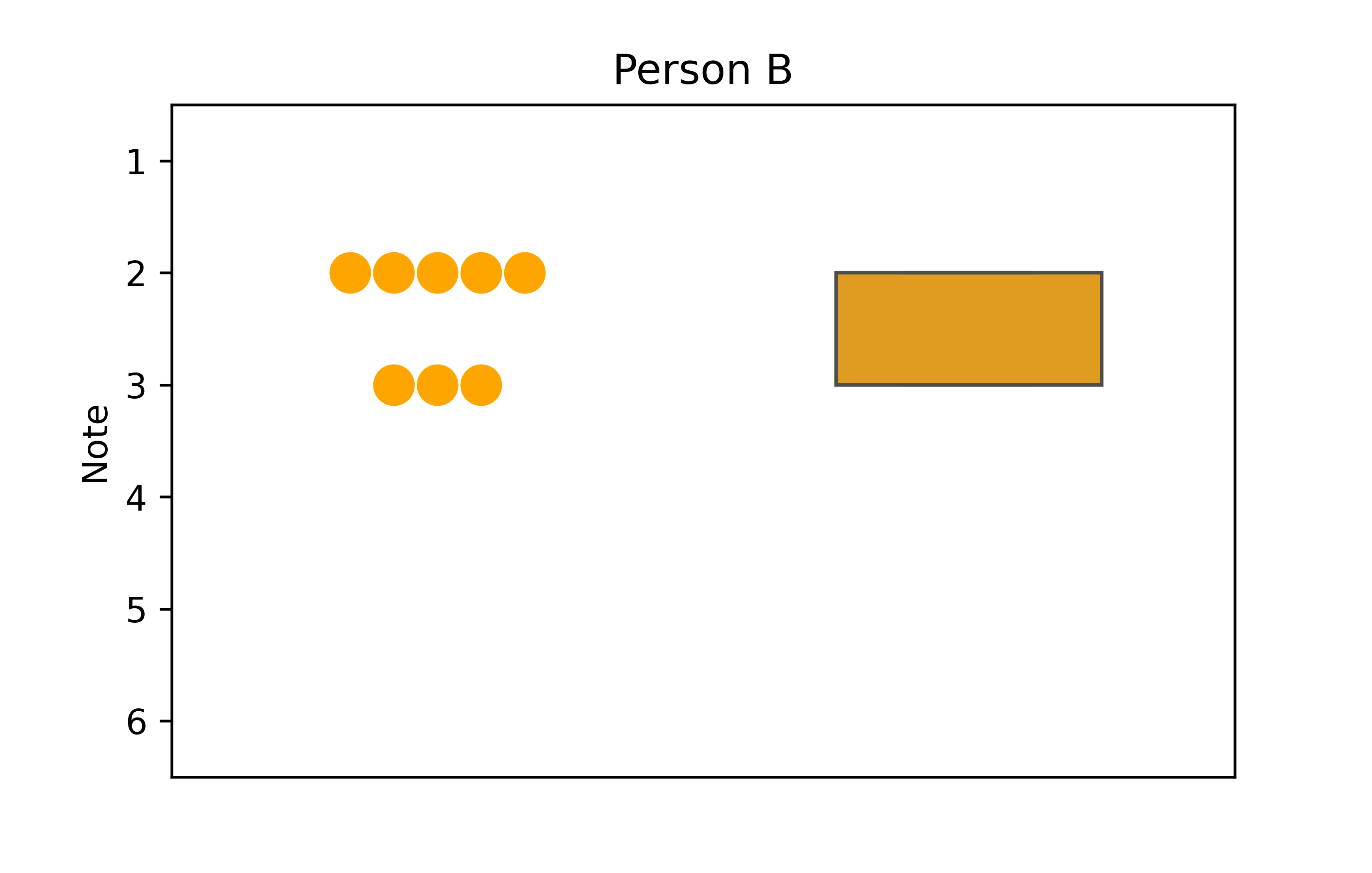
plt.figure()
plt.title('Person E')
sns.swarmplot(
x=pseudo_x,
y=noten_E,
color='firebrick',
size=12
)
sns.boxplot(
x=pseudo_x+1,
y=noten_E,
color='firebrick',
width=0.5
)
plt.yticks(np.arange(1, 7))
plt.ylim(6.5, 0.5)
plt.ylabel('Note')
plt.xlim(-0.5, 1.5)
plt.xticks([])
plt.show()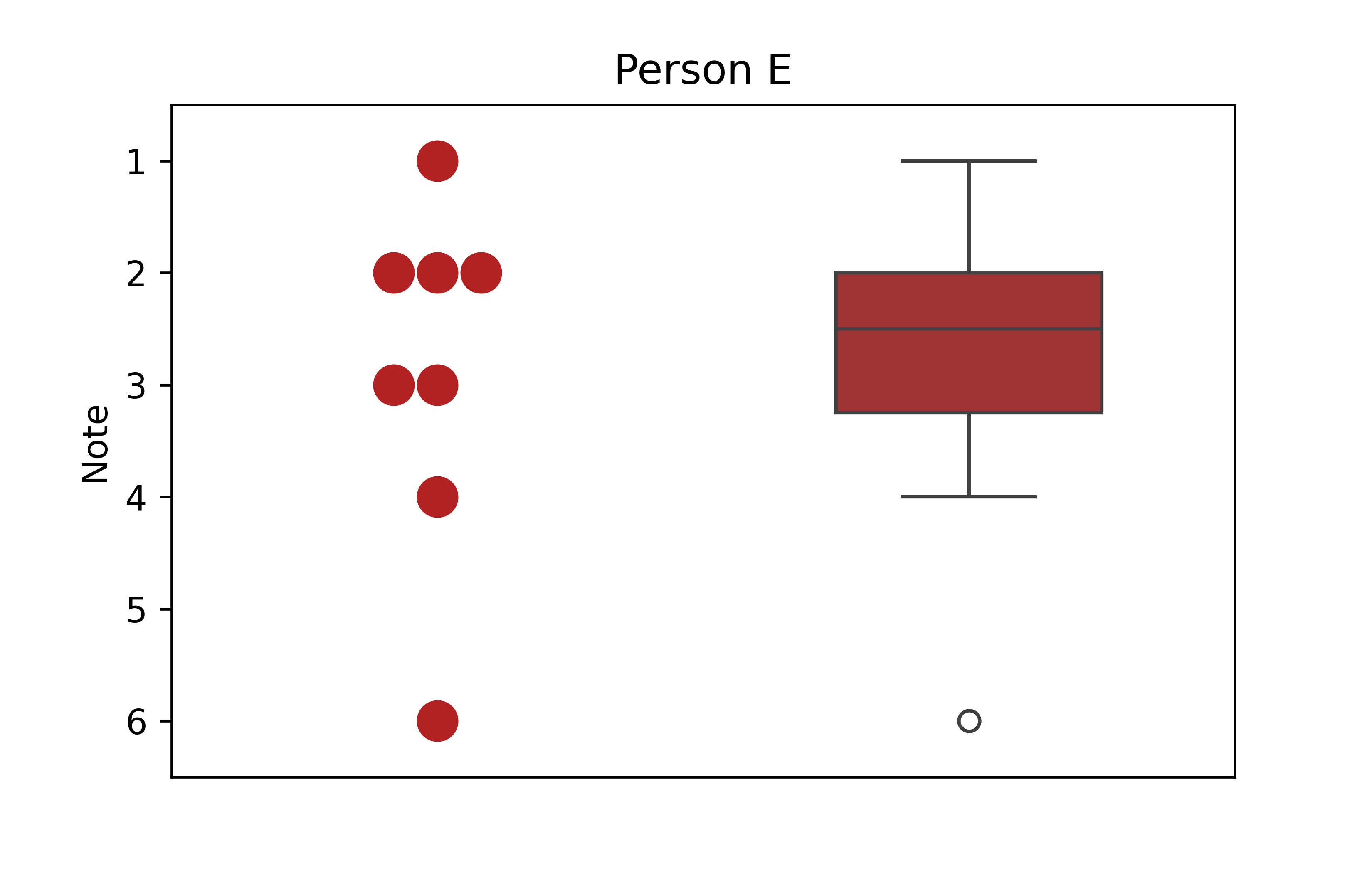
Es fällt auf, dass der Box-Plot für Person B nur aus einer Box zu bestehen scheint. Das liegt daran, dass die Daten von Person B nur aus zwei verschiedenen Noten bestehen, nämlich 2 und 3. Als Resultat sind die Spannweite und IQA identisch, sodass es keine Whisker gibt. Außerdem ist der Median auch 2, entspricht also dem Minimum, sodass es auch keine Linie innerhalb der Box gibt. Der Plot ist also korrekt gezeichnet und zeigt korrekt an, dass die Daten von Person B nicht besonders gestreut sind.
Darüber hinaus fällt auf, dass es beim Box-Plot für Person E einen Ausreißer gibt: Die Note 6. Der Ausreißer wird als einzelner Punkt außerhalb der Whisker dargestellt. Demnach endet der Whisker bei der Note 4, da die Note 6 als Ausreißer von der eigentlichen Bestimmung des Minimums und Maximums ausgeschlossen wird. Diese Einstufung ab wann ein Datenpunkt als Ausreißer gilt, wurde mit der gängigen 1,5-IQA-Regel durchgeführt. Demnach sind alle Datenpunkte, die mehr als 1,5 mal den IQA von den Quartilen entfernt sind, Ausreißer. Wie oben berechnet, gilt für Person E \(Q1=2.0\), \(Q3=3.25\) und \(IQA=1.25\). Die untere Ausreißergrenze ist also \(2.0-1.5*1.25=0.125\) und die obere Ausreißergrenze ist \(3.25+1.5*1.25=4.375\). Der kleinste Werte im Datensatz ist 1 und liegt also noch innerhalb der unteren Ausreißergrenze. Die Note 6 als größter Wert liegt allerdings außerhalb dieser Grenzen und wird als Ausreißer dargestellt.
Mittelwert ergänzen
Der Box-Plot ist also eine kompakte und informative Darstellung einiger der wichtigsten Kennzahlen einer Datenmenge. Es könnte aber bemängelt werden, dass der Mittelwert fehlt. Hin und wieder sieht man deshalb auch Box-Plots, die den Mittelwert als Punkt/Symbol innerhalb der Box einzeichnen. Das können wir auch tun, indem wir erneut die Funktion plt.scatter() nutzen, diesmal damit aber nur einen einzigen Punkt zeichnen - den Mittelwert. Als y-Wert muss alse der Mittelwert der Daten genommen werden, also y=np.mean(noten_B) bzw. y=np.mean(noten_E) und als x-Wert x=1, also die Position der Box-Plots auf der x-Achse. Neben der Farbe (color='black') ändern wir diesmal außerdem das Symbol. Anstatt einen Punkt zu zeichnen, können wir aus einer Fülle an Symbolen auswählen und entscheiden uns hier mittels marker='D' für eine Raute5 (engl. Diamond).
Schließlich lernen wir noch das Argument zorder= kennen, welches wir hier nutzen müssen um die Raute auch tatsächlich zu sehen. Dieses Argument gibt die Reihenfolge an, in der die Elemente gezeichnet werden. Ein Element mit einer höheren zorder wird also über einem Element mit einer niedrigeren zorder gezeichnet. Gibt man keine zorder an, wird eine standardmäßige Reihenfolge genutzt, die aber nicht immer zielführend ist. In unserem Fall wird die Raute sonst unter den Box-Plots gezeichnet, ist also nicht zu sehen (siehe Übungen). Wir setzen also zorder=3, also eine hohe Zahl, damit sie über den Box-Plots gezeichnet wird.
plt.figure()
plt.title('Person B')
sns.swarmplot(
x=pseudo_x,
y=noten_B,
color='orange',
size=12
)
sns.boxplot(
x=pseudo_x+1,
y=noten_B,
color='orange',
width=0.5
)
plt.scatter(
x=1,
y=np.mean(noten_B),
color='black',
marker='D',
zorder=3
)
plt.yticks(np.arange(1, 7))
plt.ylim(6.5, 0.5)
plt.ylabel('Note')
plt.xlim(-0.5, 1.5)
plt.xticks([])
plt.show()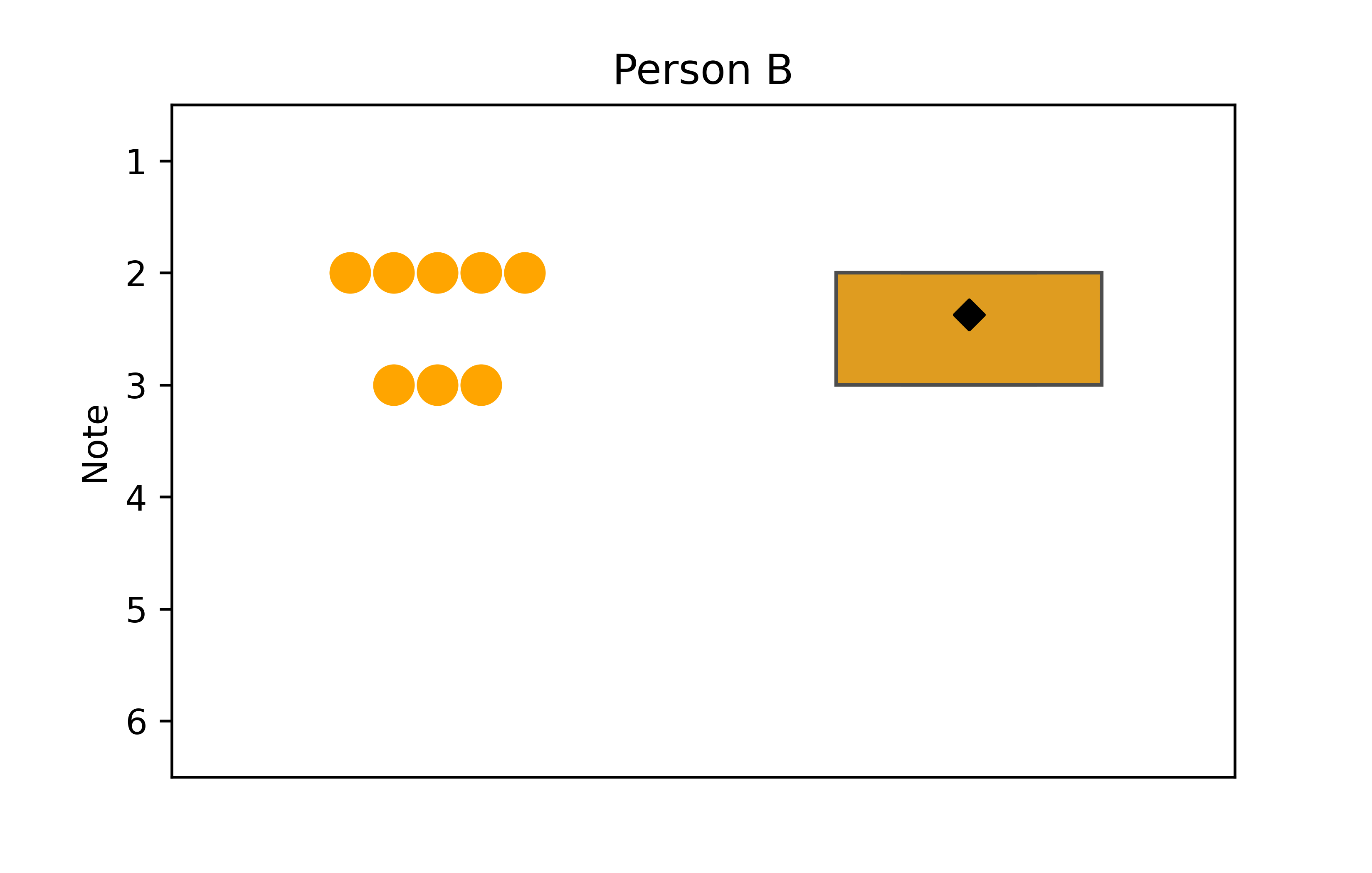
plt.figure()
plt.title('Person E')
sns.swarmplot(
x=pseudo_x,
y=noten_E,
color='firebrick',
size=12
)
sns.boxplot(
x=pseudo_x+1,
y=noten_E,
color='firebrick',
width=0.5
)
plt.scatter(
x=1,
y=np.mean(noten_E),
color='black',
marker='D',
zorder=3
)
plt.yticks(np.arange(1, 7))
plt.ylim(6.5, 0.5)
plt.ylabel('Note')
plt.xlim(-0.5, 1.5)
plt.xticks([])
plt.show()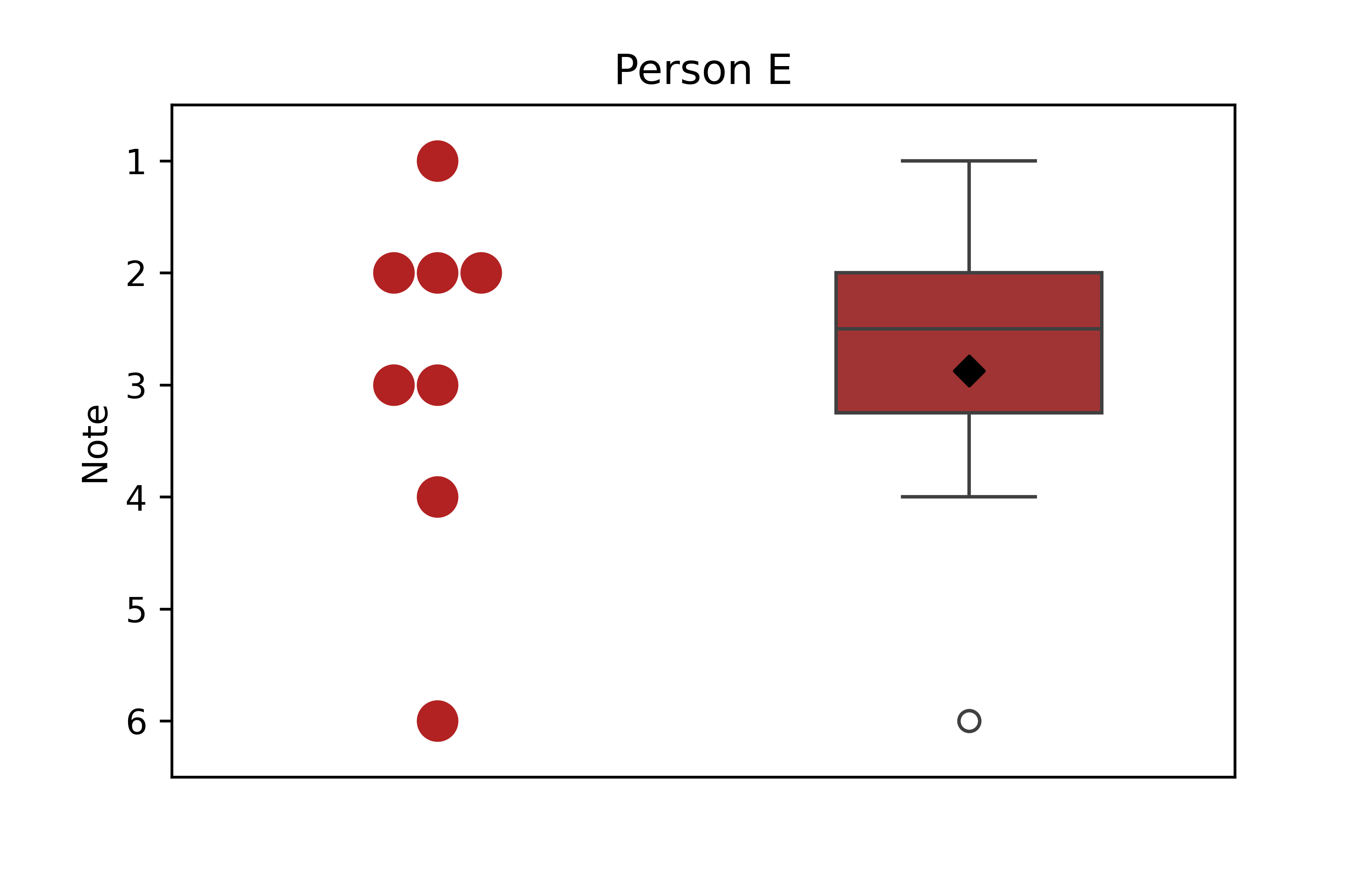
Übungen
Wie könnte man Minimum, Median und Maximum des folgenden Arrays ohne die Funktionen np.min(), np.median() und np.max() und dafür nur mit der Funktion np.quantile() berechnen?
data = np.array([1, 123, 3, 42])Minimum:
np.quantile()Median:
np.quantile()Maximum:
np.quantile()
Wähle die Variablen a, b, c und d so, dass das folgende Array mein_array jeweils eine der folgenden Bedingungen erfüllt. (Es sollen also nicht alle Bedingungen gleichzeitig erfüllt werden, sondern immer nur Werte gefunden werden, damit eine der Bedingungen erfüllt ist!)
mein_array = np.array([-3, 100, 1, a, b, c, d])- Bedingung 1: Der Median und das Minimum sind beide -3.
- Bedingung 2: Der Box-Plot hat Whisker auf beiden Seiten.
- Bedingung 3: Der Box-Plot hat nur auf einer Seite einen Whisker.
- Bedingung 4: Der Box-Plot hat keine Whisker.
Erzeuge einen Plot ähnlich des letzten in diesem Kapitel, also mit Dot-Plot, Box-Plot und Mittelwert als Raute. Zeichne jedoch alle Elemente übereinander, also auf dieselbe x-Position 0. Nutze dann zorder= nicht nur in plt.scatter(), sondern in allen drei Funktionen, um die Reihenfolge der Elemente zu verändern. Ziel ist es, dass jedes der drei Elemente einmal im Vordegrund ist, also über den anderen Elementen gezeichnet wird.
Anstatt den Mittelwert als Punkt/Raute einzufügen, könnten wir ihn natürlich auch wieder als gestrichelte rote Linie einfügen - so wie wir es bei den Histogrammen getan haben. Füge also eine gestrichelte rote Linie für den Mittelwert ein. Hinweis: Das v in dem Befehl, den wir zum Einfügen der Linie bei den Histogrammen genutzt haben, steht für vertikal.
Fußnoten
Terzile teilen die Daten in drei Teile. Das 0,33-Quantil ist das 1. Terzil, das 0,66-Quantil ist das 2. Terzil.↩︎
Quintile teilen die Daten in fünf Teile. Das 0,2-Quantil ist das 1. Quintil, das 0,4-Quantil ist das 2. Quintil, das 0,6-Quantil ist das 3. Quintil, das 0,8-Quantil ist das 4. Quintil.↩︎
Dezile teilen die Daten in zehn Teile. Das 0,1-Quantil ist das 1. Dezil, das 0,2-Quantil ist das 2. Dezil, das 0,3-Quantil ist das 3. Dezil, usw.↩︎
Perzentile teilen die Daten in hundert Teile. Das 0,01-Quantil ist das 1. Perzentil, das 0,02-Quantil ist das 2. Perzentil usw.↩︎
Meines Erachtens eignet sich z.B. die Raute besonders gut, da sie genau in der Mitte des Symbols Ecken hat, die also den Wert exakt anzeigen - unabhängig der Größe des Symbols. Ein Plus hätte diese Eigenschaft beispielsweise auch, ein Quadrat hingegen nicht.↩︎