import numpy as np
import matplotlib.pyplot as pltMittelwert und Histogramm
Mittelwerte und Histogramme gehören nicht zwangsläufig zusammen, aber dieses Kapitel ist eine gute Gelegenheit, um beides zu behandeln.
Mittelwert
Wenn man vom im deutschen von “Mittelwert”, “Mittel”, “Durschschnitt”, “Schnitt” oder im englischen von “mean” oder “average” spricht, meint man in der Regel1 den “arithmetischen Mittelwert”. Dieser wird berechnet, indem alle Werte addiert und durch die Anzahl der Werte geteilt werden. Es ist die im Alltag wohl gängigste statistische Kennzahl. So haben beispielswiese alle in ihrer Schulzeit den Durchschnitt ihrer Noten berechnet. Hier ist ein entsprechendes Beispiel mit NumPy:
noten_A = np.array([2, 3, 4, 2, 1, 2, 3, 2])
mw_A = np.mean(noten_A)
print(mw_A)2.375Der Notenschnitt ist hier also 2,375. Es ist selbstverständlich, dass diese Information schneller und leichter zu verstehen ist, als sich die ganze Notenliste anzusehen. Gleichzeitig muss aber klar sein, dass auch Informationen über die Noten verloren gehen, wenn man nur den Mittelwert betrachtet. Das wird deutlich, wenn wir eine weitere Notenliste hinzunehmen:
noten_B = np.array([2, 3, 3, 2, 2, 2, 3, 2])
mw_B = np.mean(noten_B)
print(mw_B)2.375Auch hier ist der Notenschnitt 2,375, allerdings hatte Person B im Gegensatz zu Person A keine einzige 1 oder 4, sondern ausschließlich 2en und 3en. Auffälligkeiten wie diese bilden den Kern der Motivation dafür sich nicht nur eine Kennzahl, sondern mehrere anzuschauen. In diesem Fall handelt es sich lediglich um eine interessante Randnotiz, aber in anderen Fällen kann es sehr wichtig sein genau solche Unterschiede in den Daten herauszuarbeiten.
Wir wollen die beiden Notenlisten nun auch grafisch darstellen, um die Unterschiede besser zu sehen. Unser erstes Diagramm wird ein Histogramm sein.
Ein Histogramm (engl. histogram) ist eine Art Balken-/Säulendiagramm, das die Häufigkeit von Werten in bestimmten Intervallen darstellt. Normalerweise sind alle Intervalle gleich groß, aber das ist nicht zwingend notwendig. Auf der y-Achse können entweder die absoluten Häufigkeiten oder die relativen Häufigkeiten (in Prozent) dargestellt werden.
Um mit Matplotlib ein Histogramm zu erstellen, verwenden wir die Funktion plt.hist().
plt.figure()
plt.hist(noten_A, bins=[0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5])
plt.show()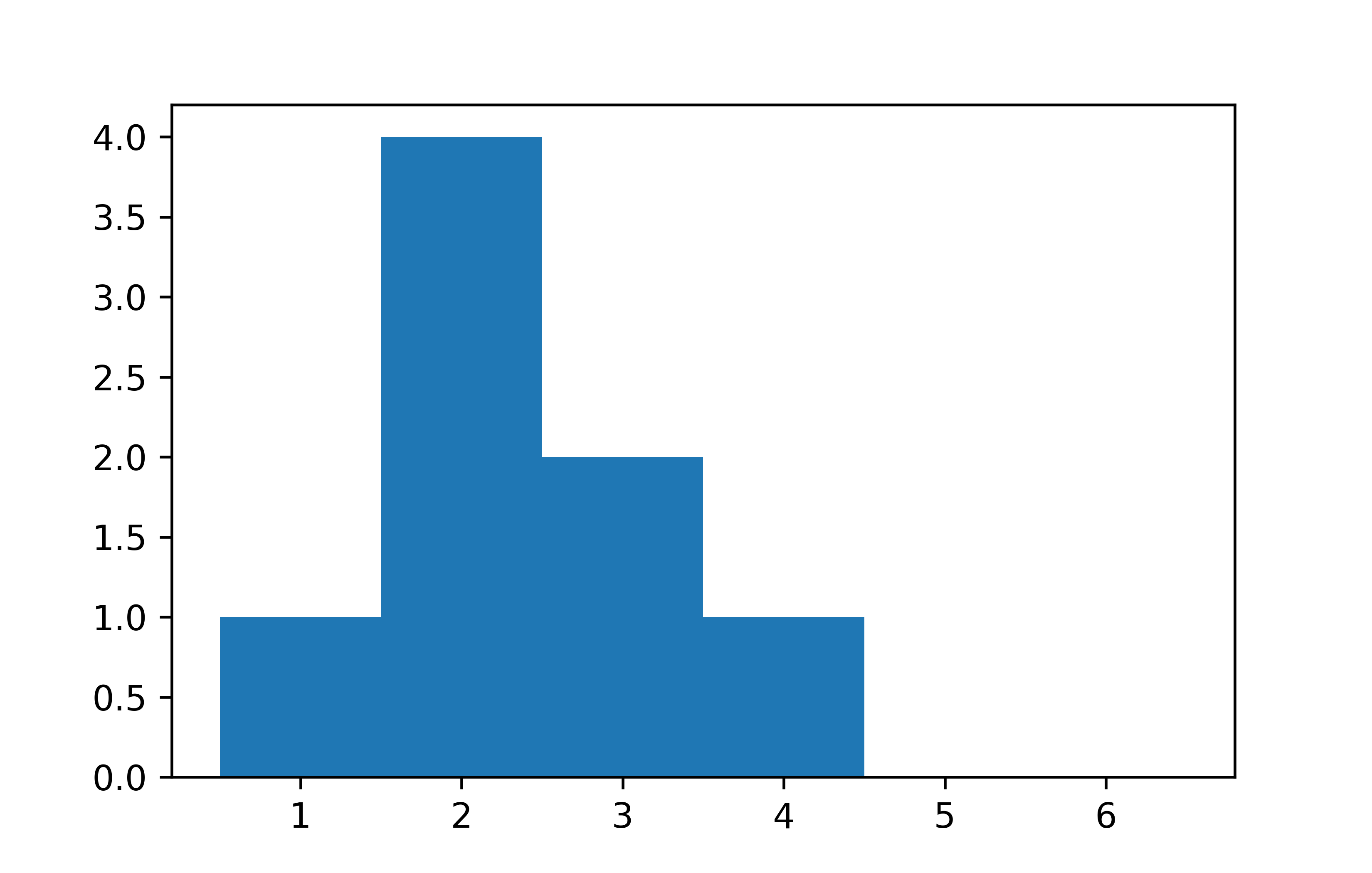
Zur Erinnerung: Wir haben oben matplotlib.pyplot als plt importiert. Matplotlib ist eine Bibliothek mit mehreren Modulen und wir nutzen also das Modul pyplot mittels des gängigen Kürzels plt. Das Modul hat viele Funktionen, die wir nicht alle und nur nach und nach kennenlernen werden. Die eigentliche Funktion zur Erzeugung eines Histograms ist wie gesagt plt.hist(). Wir rufen aber auch direkt vorher die Funktion plt.figure() auf, um ein neues, leeres Diagramm zu erstellen. Das ist nicht zwingend notwendig, aber es ist eine gute Gewohnheit, die wir uns früh aneignen wollen. Am Ende rufen wir plt.show() auf, um das Diagramm anzuzeigen.
Wir haben also die Notenliste noten_A als erstes Argument an plt.hist() übergeben, damit die Funktion Daten hat, die sie zeichnen kann. Die Funktion würde auch ohne das zweite Argument funktionieren, da sie dann automatisch Intervalle berechnet. Diese automatisch gewählten Intervalle sind allerdings für speziell diese Daten nicht zielführend, weshalb wir die Intervalle manuell angeben. Im englischen heißen die Intervalle und deshalb auch das Argument bins. Die Intervallgrenzen sind hier so gewählt, dass die Noten 1 bis 6 jeweils mittig in einem Intervall liegen.
Wir können nun beschließen Histogramme für Person A und Person B zu erzeugen und sie nebeneinander zu legen. In diesem Zug wollen wir direkt drei Vorkehrungen treffen:
- Die Intervalle sollten vorher in eine Variable
noten_binsgespeichert werden, damit wir sie nicht mehrfach eingeben müssen. - Die Füllfarbe der Balken soll sich unterscheiden, damit wir die beiden Histogramme besser auseinanderhalten können. Person A bekommt die Farbe
royalblueund Person B die Farbeorange2. Dazu nutzen wir das Argumentcolor. - Die Balken sollen einen schwarzen Rand bekommen, damit sie sich besser abheben. Dazu nutzen wir das Argument
edgecolor.
noten_bins = [0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5]plt.figure()
plt.hist(
noten_A,
bins=noten_bins,
color='royalblue',
edgecolor='black'
)
plt.show()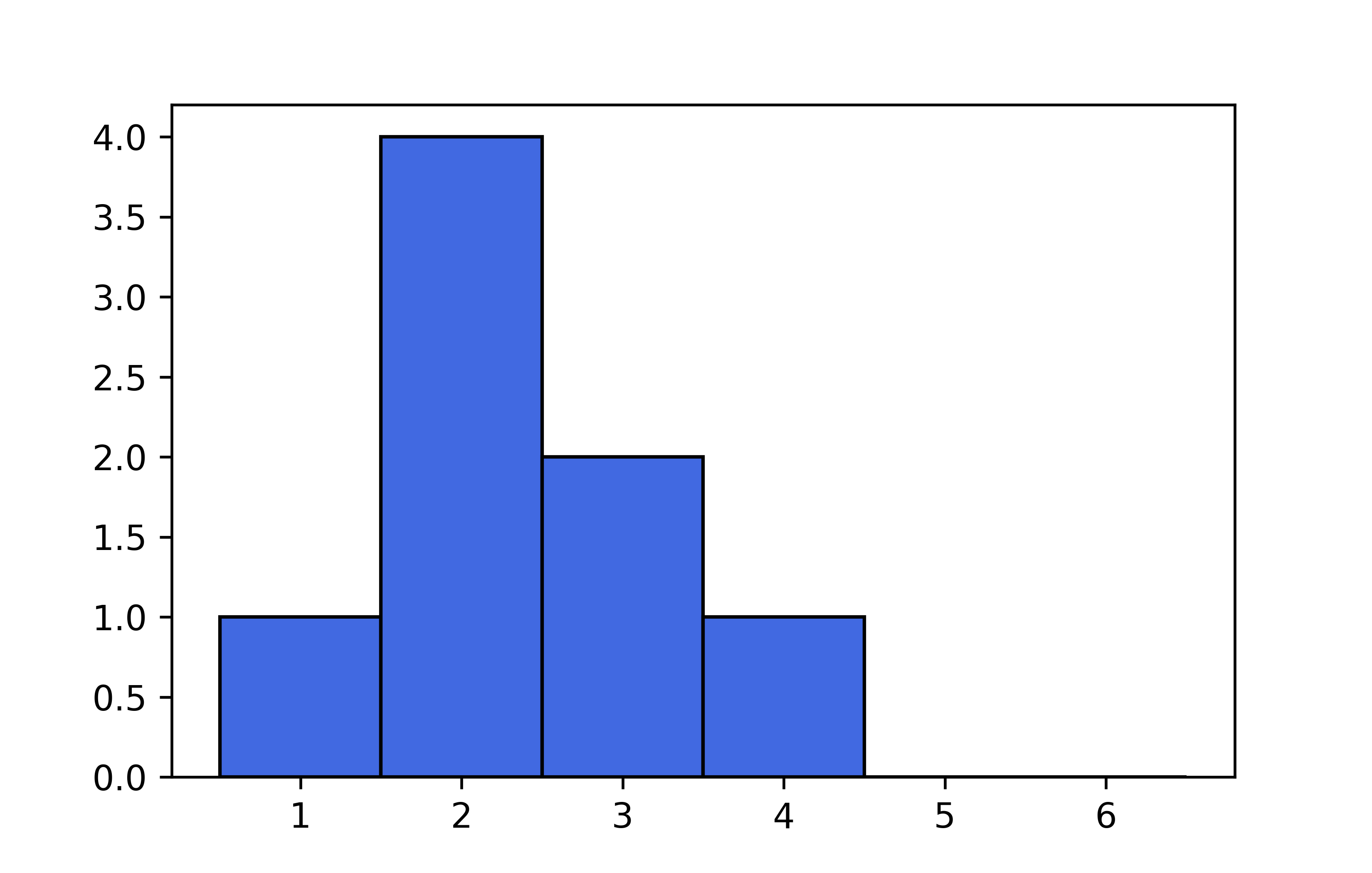
plt.figure()
plt.hist(
noten_B,
bins=noten_bins,
color='orange',
edgecolor='black'
)
plt.show()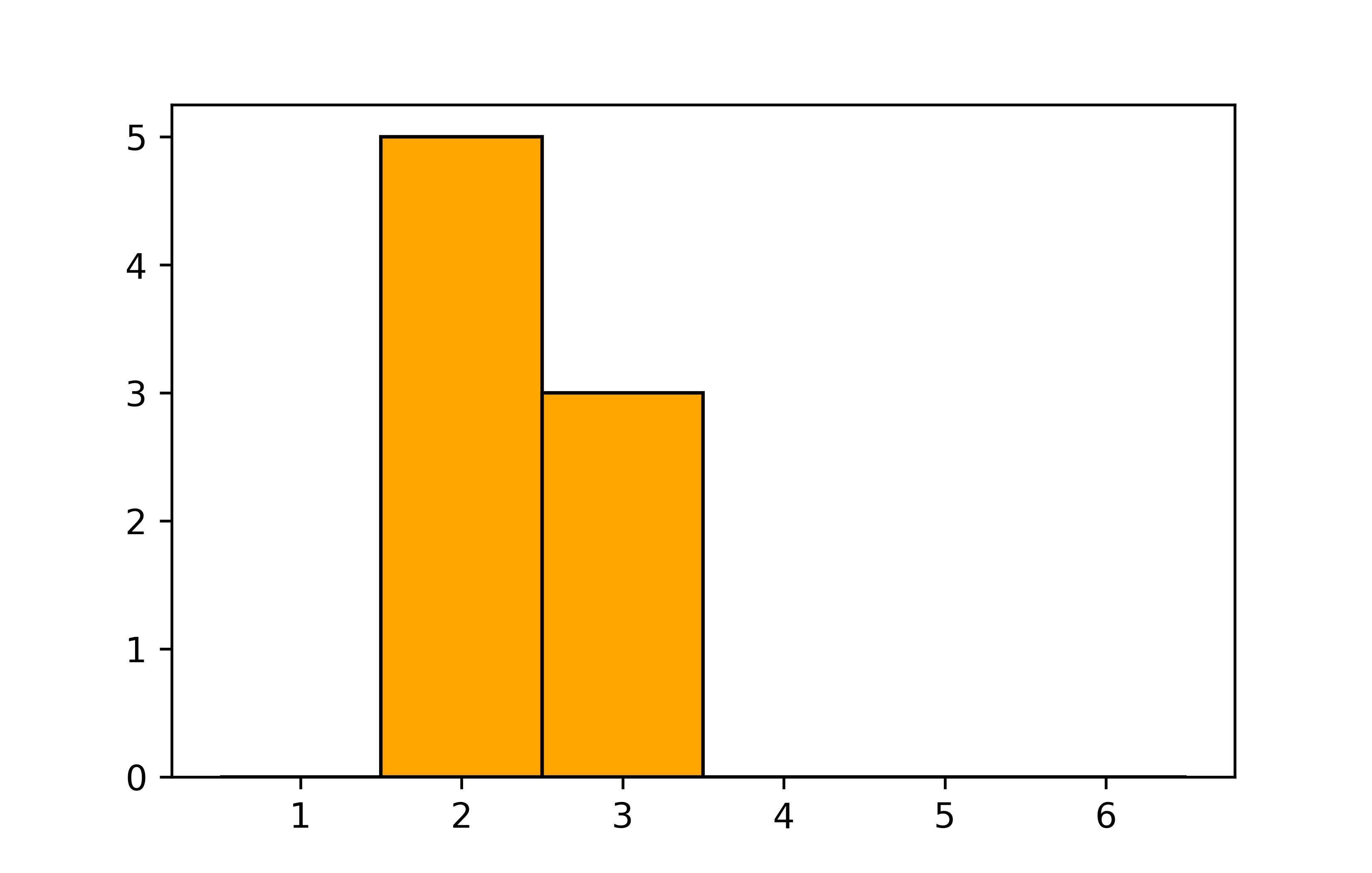
Diese beiden Diagramme zeigen schon deutlich, dass die beiden Notenlisten unterschiedlich sind. Person A hat eine 4 und eine 1, Person B hat keine 4 und keine 1. Da beide gleich viele Noten erhalten haben, hat Person B dementsprechend mehr 2en und 3en. Speziell bzgl. des höchsten Balkens - dem der 2en - sieht man das bisher aber nicht unbedingt sofort. Das liegt daran, dass die y-Achse je Plot unterschiedlich skaliert ist - nämlich jeweils so, dass es keinen unnötigen leeren Raum über dem höchsten Balken gibt. Das ist in der Regel ein gutes Standarverhalten von Matplotlib, aber in diesem Fall wollen wir die y-Achse gleich skalieren, um die beiden Diagramme besser vergleichen zu können. Dazu nutzen wir die Funktion plt.ylim(). Diese Funktion nimmt zwei Argumente entgegen, die die untere und obere Grenze der y-Achse festlegen.
Außerdem wollen wir den Plots noch Titel geben, um sie besser auseinanderhalten zu können. Dazu nutzen wir die Funktion plt.title(). Im Gegensatz zu den Farbänderungen, die wir oben mittels Argumenten an die Funktion plt.hist() übergeben haben, sind plt.ylim() und plt.title() weitere Funktionen, die wir zusätzlich zu plt.hist() aufrufen. Das liegt daran, dass diese Funktionen nicht nur für das Histogramm, sondern für das gesamte Diagramm gelten. Die Reihenfolge dieser Aufrufe ist dabei relativ flexibel - so könnte der Titel auch nach plt.hist() festgelegt werden.
plt.figure()
plt.title('Person A')
plt.hist(
noten_A,
bins=noten_bins,
color='royalblue',
edgecolor='black'
)
plt.ylim(0, 5.5)
plt.show()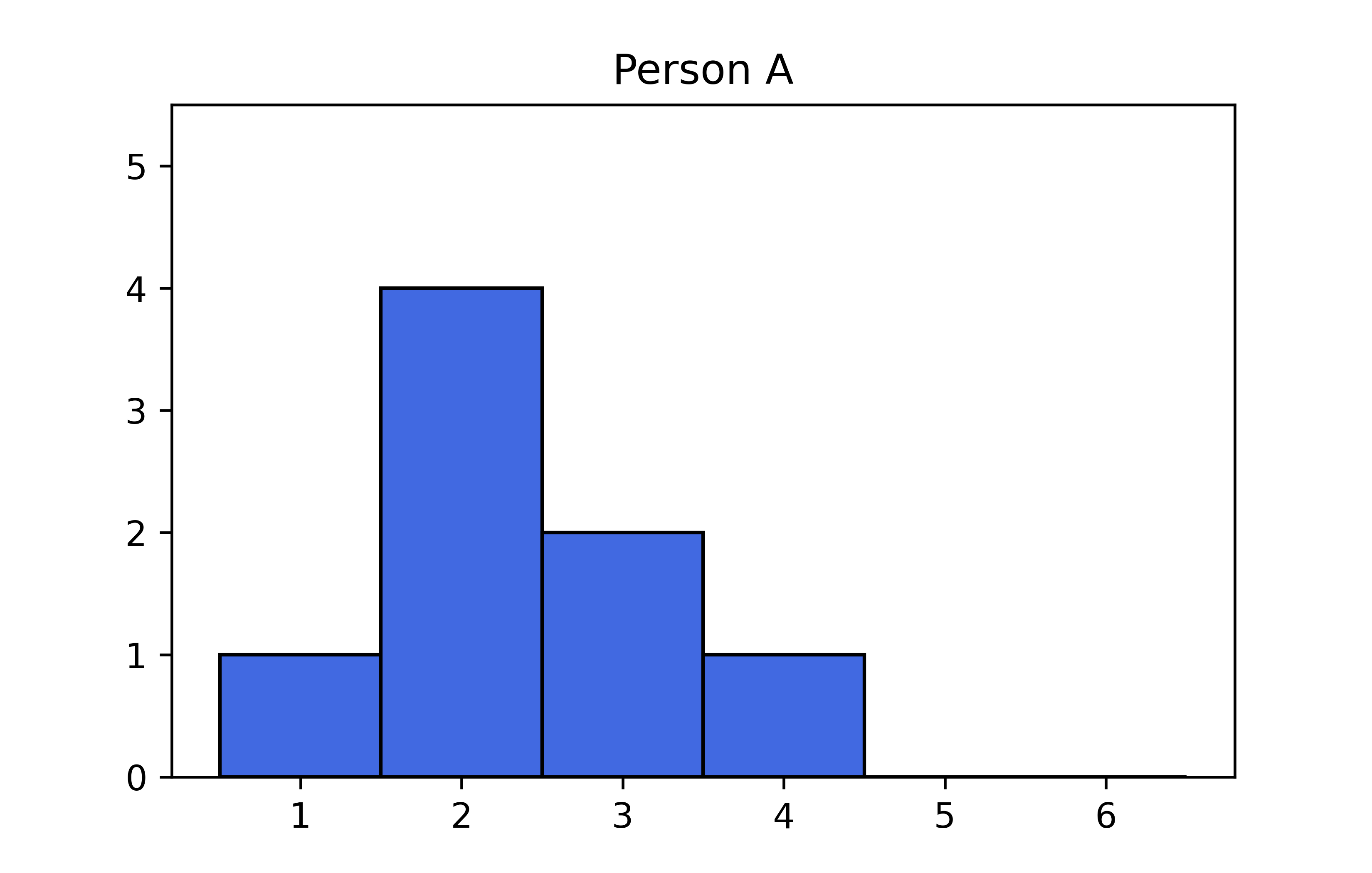
plt.figure()
plt.title('Person B')
plt.hist(
noten_B,
bins=noten_bins,
color='orange',
edgecolor='black'
)
plt.ylim(0, 5.5)
plt.show()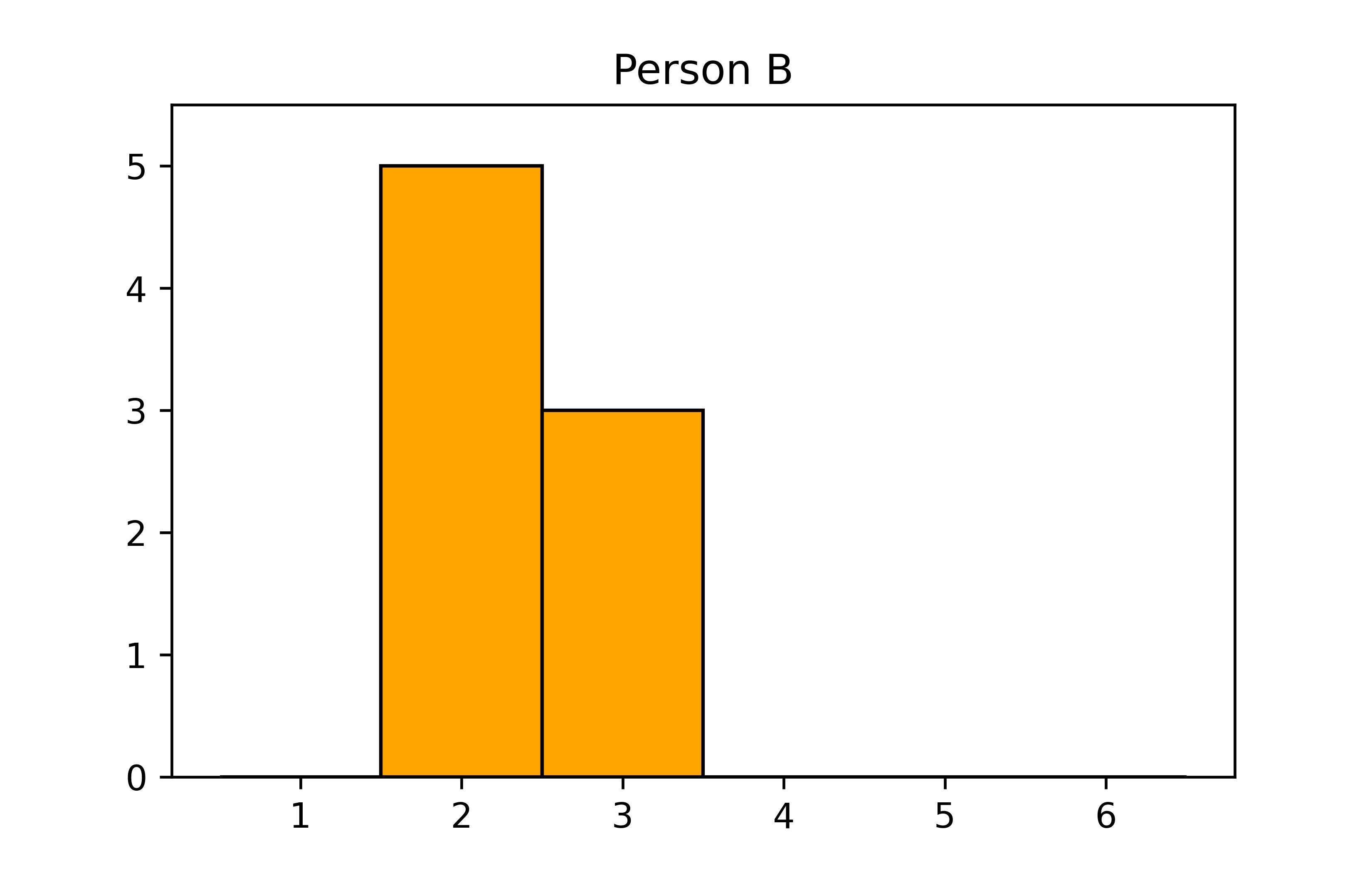
Schließlich wollen wir noch die Achsen beschriften und die Mittelwerte als vertikale Linien einzeichnen. Für die Beschriftungen nutzen wir die Funktionen plt.xlabel() und plt.ylabel(). Für die Linien nutzen wir die Funktion plt.axvline(). Diese Funktion zeichnet eine vertikale Linie an einer bestimmten x-Position. Die Position ist hier der Mittelwert, den wir mit plt.axvline() als erstes Argument übergeben. Die Linien sollen in diesem Fall die Farbe black und die Linienart dashed haben. Dazu nutzen wir die Argumente color und linestyle.
plt.figure()
plt.title('Person A')
plt.hist(
noten_A,
bins=noten_bins,
color='royalblue',
edgecolor='black'
)
plt.axvline(
mw_A,
color='black',
linestyle='dashed'
)
plt.xlabel('Noten')
plt.ylabel('Anzahl')
plt.ylim(0, 5.5)
plt.show()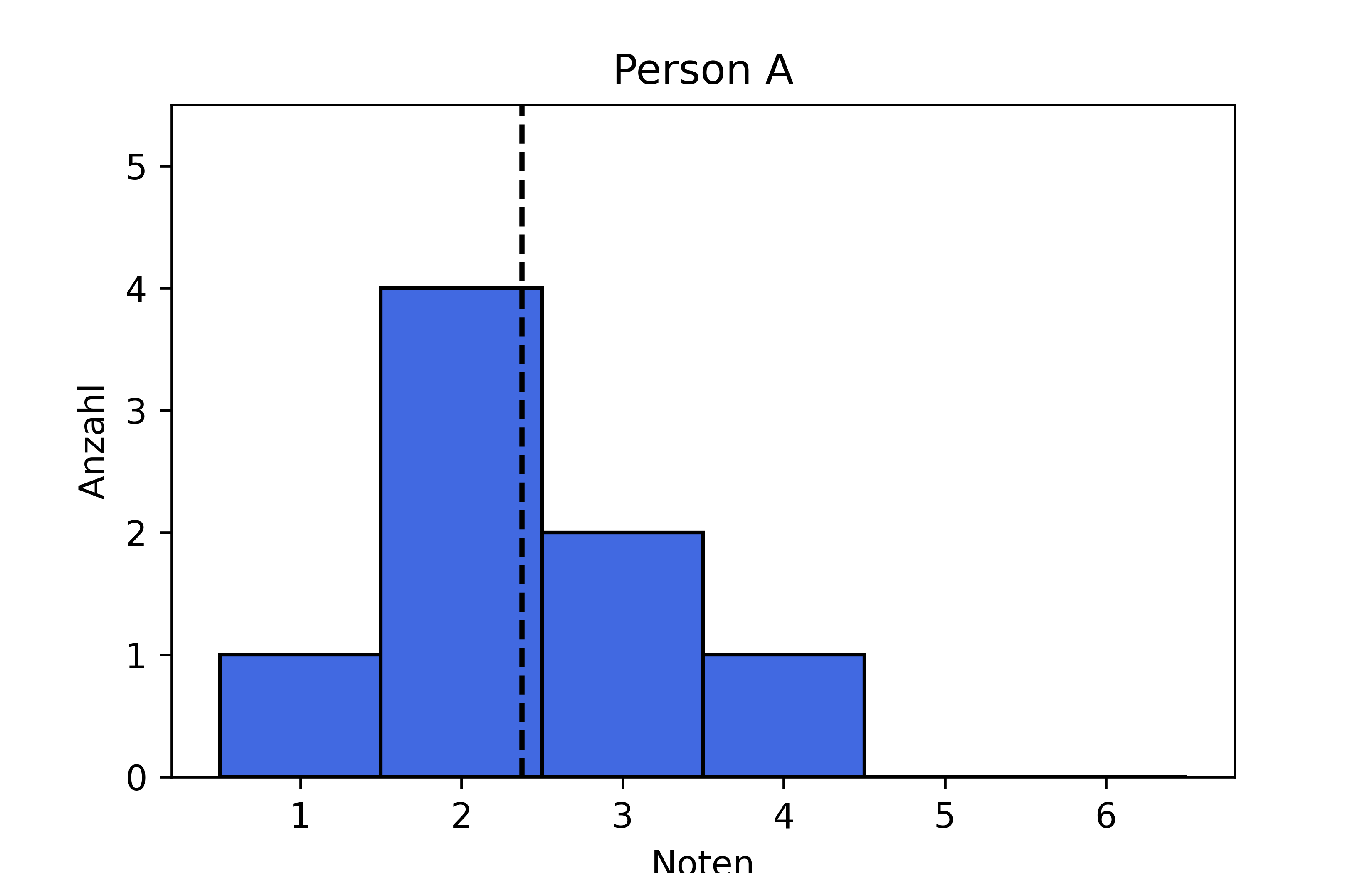
plt.figure()
plt.title('Person B')
plt.hist(
noten_B,
bins=noten_bins,
color='orange',
edgecolor='black'
)
plt.axvline(
mw_B,
color='black',
linestyle='dashed'
)
plt.xlabel('Noten')
plt.ylabel('Anzahl')
plt.ylim(0, 5.5)
plt.show()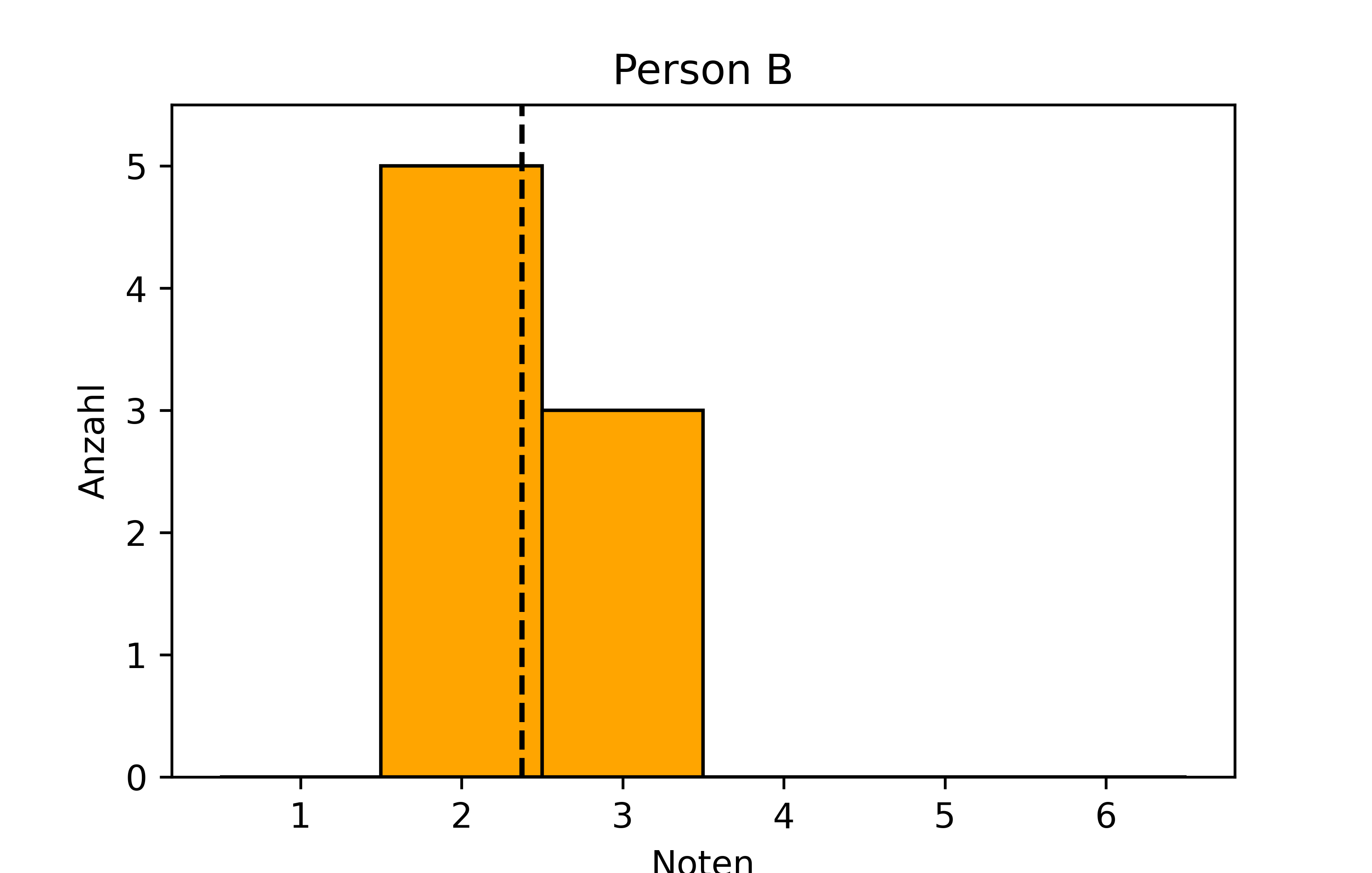
Hier wollen wir das Kapitel erstmal beenden. Wir haben uns mit dem Mittelwert und dem Histogramm beschäftigt und dabei auch schon einige wichtige Funktionen von Matplotlib kennengelernt. Gleichzeitig konnten wir mit den Histogrammen gut herauskristallisieren, wie der Mittelwert alleine ggf. nicht ausreicht, um Daten vollständig zu verstehen.
In den nächsten Kapiteln werden wir uns mit dem Median und Quantilen beschäftigen und dabei zwei neue Diagrammtypen kennenlernen: Streudiagramme und Box-Plots.
Übungen
Zeichne Histogramm für die Notenliste noten_A jeweweils mit folgenden Änderungen und schaue was passiert:
- ohne die Intervalle mit dem Argument
binszu definieren - mit den Intervallen
bins = [1, 2, 3, 4, 5, 6] - Wähle aus dieser Liste andere Farben für die Balken und den Rand.
- Wähle aus dieser Liste andere Linienarten für die vertikalen Linien.
Zeichne die Histogramme nochmals mit relativ skalierten y-Achsen, also Anteil/Prozent statt der absoluten Anzahl. Dafür sollen nicht vorher Prozentzahlen ausgerechnet werden, sondern lediglich ein Argument der plt.hist() Funktion genutzt werden. Zur Übung soll das Argument hier in der Online-Dokumentation von Matplotlib gesucht werden. Tip: es ist ein Argument, das man auf True setzen muss. Hinweis: die y-Limits und das y-Label sollten dann auch angepasst werden.
Welche Note fehlt hier, damit auch dieser Notenschnitt derselbe ist wie die von den Personen A und B?
np.array([1, 6, 1, 6, 1, , 1, 1])
Fußnoten
Es gibt auch andere Mittelwerte, wie das geometrische Mittel, das harmonische Mittel oder das quadratische Mittel. Diese sind aber in der Praxis deutlich seltener und werden hier nicht weiter behandelt. Mehr dazu hier.↩︎
Diese Farben sind in Matplotlib so als Strings definiert, es können aber auch Hexadezimalwerte oder RGB-Werte angegeben werden. Später mehr dazu.↩︎