import numpy as np
import matplotlib.pyplot as plt
import seaborn as snsPunktdiagramme
Nachdem wir nun Mittelwert und Median eingeführt und mithilfe von Histogrammen visualisiert haben, wollen wir uns nun mit weiteren Visualisierungen beschäftigen. Neben Balken-/Säulendiagrammen (zu denen Histogramme gehören) werden häufig auch Punkte in Diagrammen verwendet. Mit solchen Diagrammen sind hier also alle Diagramme gemeint, in denen Datenpunkte als Punkte (bzw. Symbole) dargestellt werden. Das wohl bekannteste dieser Diagramme ist das Streudiagramm.
Ein Streudiagramm (auch: Punktewolke, Scatterplot) ist ein Diagramm, das i.d.R. zwei Variablen in einem zweidimensionalen Koordinatensystem darstellt. Jeder Punkt im Diagramm repräsentiert dann ein Paar von Werten.
Um ein Streudiagramm zu zeichnen, nutzen wir die Funktion plt.scatter(). Diese Funktion erwartet zwei Argumente: x mit Werten für die x-Achse und y mit Werten für die y-Achse. Hier ein Beispiel mit möglichst wenig Code und Daten, die sonst nichts mit diesem Kapitel zu tun haben:
x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
y = [1, 4, 9, 16, 25, 36, 49, 64, 81, 100]
plt.figure()
plt.scatter(x, y)
plt.show()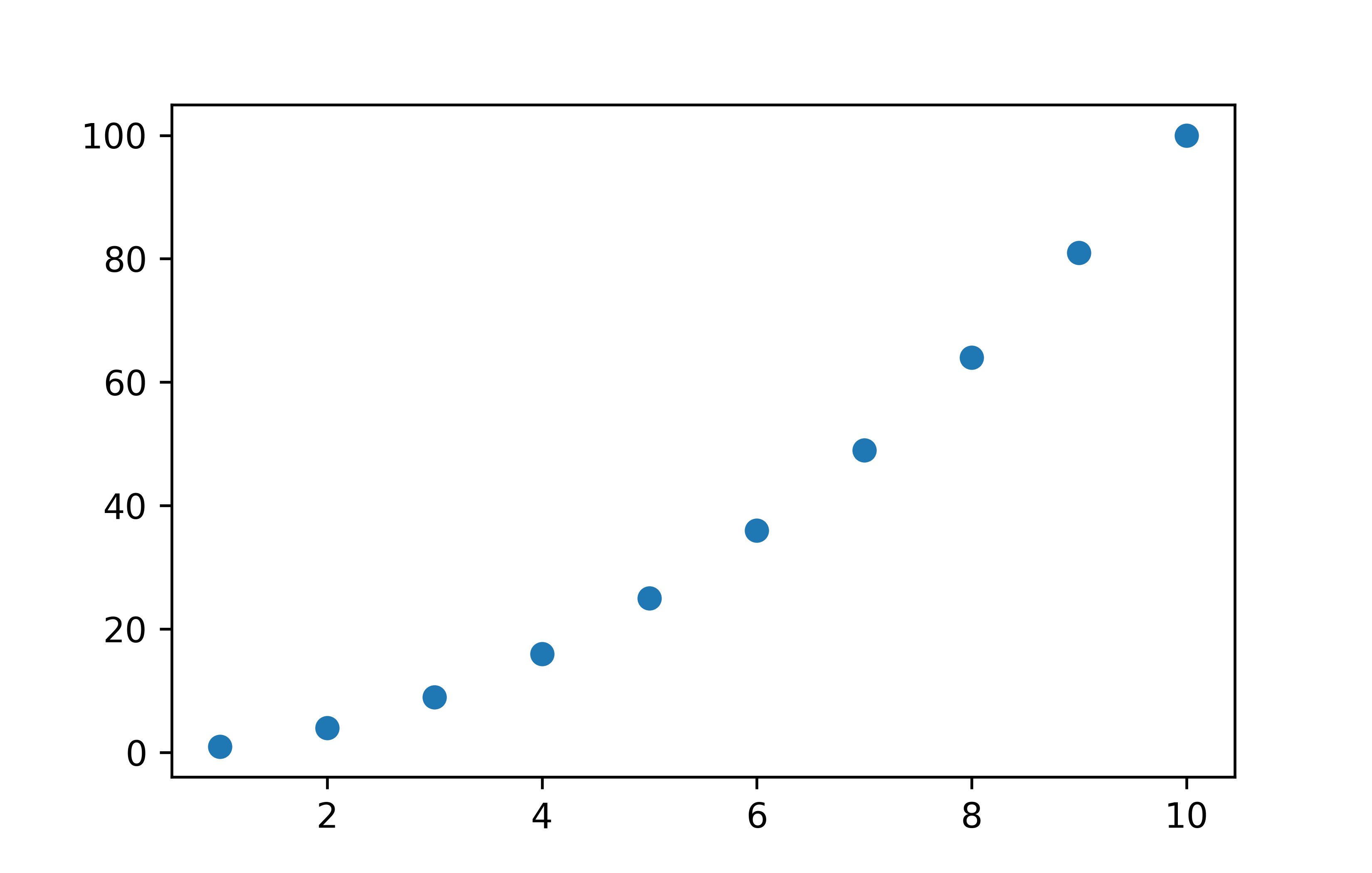
Da in unserem Fall pro Person lediglich eine Variable vorliegt, nämlich die Noten, könnte man argumentieren, dass ein Streudiagramm nicht die ideale Darstellungsform ist. Wir wollen hier aber dennoch ein Punktdiagramm zeichnen, da wir dabei u.a. ein besseres Verständnis für die demnächst folgenden Box-Plots bekommen. Diesmal betrachten wir wieder die Noten der Personen A und B.
noten_A = np.array([2, 3, 4, 2, 1, 2, 3, 2])
mw_A = np.mean(noten_A)
median_A = np.median(noten_A)
print(mw_A)
print(median_A)2.375
2.0noten_B = np.array([2, 3, 3, 2, 2, 2, 3, 2])
mw_B = np.mean(noten_B)
median_B = np.median(noten_B)
print(mw_B)
print(median_B)2.375
2.0Um also unser quasi eindimensionales Streudiagramm zu zeichnen, legen wir die Noten auf die y-Achse und setzen die x-Werte alle auf einen konstanten Wert, z.B. auf 0. Letzteres können wir mit der Funktion np.zeros() erreichen, die uns ein Array mit lauter Nullen in der Länge des übergebenen Arrays erstellt. Wir brauchen genau so viele x-Werte, wie wir Noten übergeben, also erzeugen wir ein Array mit lauter Nullen in der Länge des Noten-Arrays und nennen es pseudo_x.
pseudo_x = np.zeros(len(noten_A))plt.figure()
plt.scatter(x=pseudo_x, y=noten_A)
plt.show()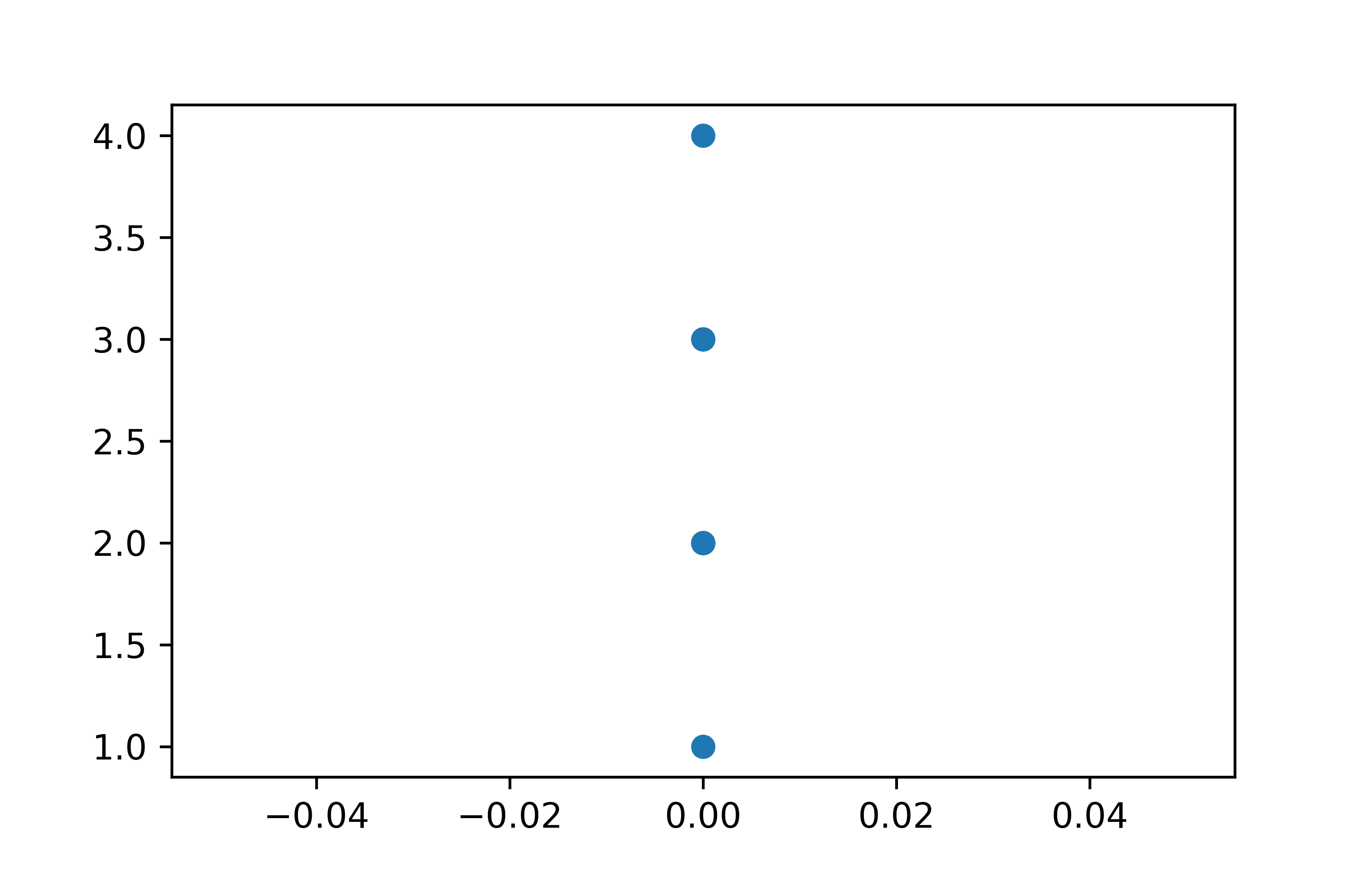
print(noten_A)
print(pseudo_x)[2 3 4 2 1 2 3 2]
[0. 0. 0. 0. 0. 0. 0. 0.]Der erzeugte Plot mag auf den ersten Blick eigenartig oder gar falsch aussehen. Wir sehen nur vier Punkte obwohl wir doch 8 Noten plotten wollten, die y-Achse geht von 1,0 bis 4,0 und die x-Achse von 0,96 bis 1,04. Tatsächlich ist aber alles korrekt. Person A hatte in der Tat vier verschiedene Noten, nämlich 1, 2, 3 und 4 und die x-Werte sind alle 1. Die Achsen sind lediglich ungünstig skaliert bzw. formatiert. Der Grund warum wir vier und nicht acht Punkte sehen ist, dass alle Punkte derselben Note genau aufeinander liegen.
Wir wollen erstmal das Problem mit den Achsen lösen. Die y-Achse sollte nur die Werte 1-6 enthalten und zwar im Idealfall mit der 1 oben und der 6 unten. Das erreichen wir mit einer Kombination aus plt.yticks() und plt.ylim(). Wir setzen die Ticks der y-Achse mit plt.yticks() auf np.arange(1, 7) und setzen die Limits der Achse mit plt.ylim() auf 6,5 und 0,5 - fügen also etwas Platz oben und unten hinzu und forcieren gleichzeitig die Reihenfolge der Ticks, da wir ja als unteres Limit die größere Zahl 6,5 und als oberes Limit die kleinere Zahl 0,5 setzen.
Die x-Achse hingegen wollen wir gar nicht sehen, also setzen wir die Ticks mit plt.xticks() auf eine leere Liste. Außerdem ergänzen wir noch einen Titel und y-Label.
plt.figure()
plt.title('Person A')
plt.scatter(x=pseudo_x, y=noten_A)
plt.yticks(np.arange(1, 7))
plt.ylim(6.5, 0.5)
plt.ylabel('Note')
plt.xticks([])
plt.show()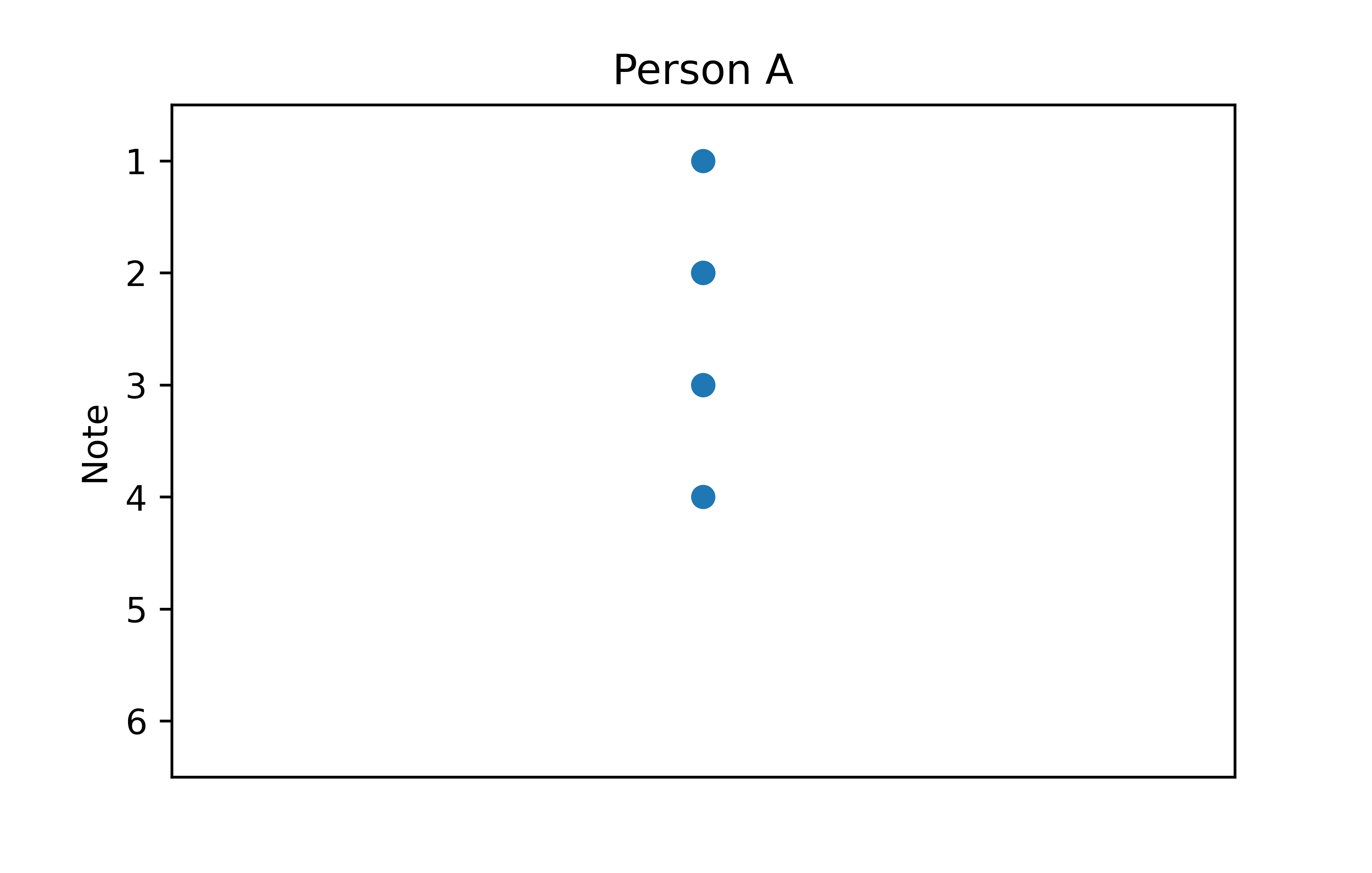
Diese Abbildung ist schon deutlich besser. Nun gilt es aber das Problem mit den überlappenden Punkten zu lösen. Dieses Problem tritt in der Praxis häufig auf und ist dann nicht immer so offensichtlich wie hier. Wird es nicht bemerkt, kann es die Interpretation des Diagramms verfälschen. Selbst mit dem Wissen, dass insgesamt 8 Noten vorliegen, gibt uns das Diagramm in der jetzigen Form keinerlei Anhaltspunkt dafür ob Person A nur eine oder mehrere 1en bekommen hat.
Es gibt nicht nur eine Lösung für dieses Problem und wir werden in zukünftigen Kapiteln darauf zurückkommen. Die Lösung, die wir hier anwenden, ist die Verwendung eines sogenannten Dot-Plots.
Ein Dot-Plot (auch1: Schwarmdiagramm, Swarm plot, Beeswarm plot) ist eine spezielle Form des Streuungsdiagramms, bei dem Punkte so im Diagramm platziert werden, dass sie die Verteilung der Datenpunkte darstellen, ohne sich zu überlappen. Unter gewissen Umständen kann ein Dot-Plot einem Histogramm ähneln, wobei die Balken durch aneinandergereihte Punkte ersetzt werden.
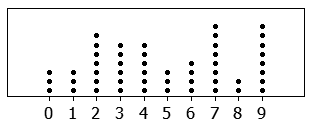
Dot-Plot Beispiel 1. Quelle: Wikipedia
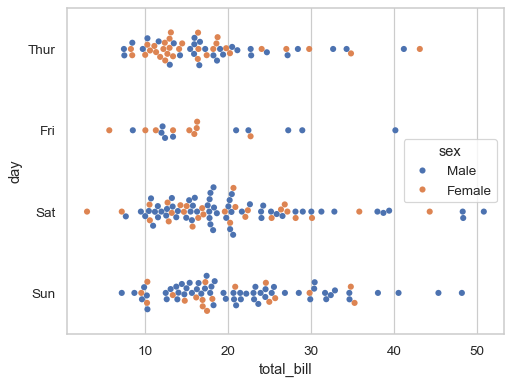
Dot-Plot Beispiel 2. Quelle: Seaborn Dokumentation
Leider bietet die Bibliothek matplotlib keine Funktion, um Dot-Plots zu zeichnen. Wir können aber auf das Modul seaborn zurückgreifen, das bereits in den vorherigen Kapiteln als Erweiterung von matplotlib erwähnt wurde. Auch hier ist es nicht nötig seaborn zu installieren, da es wie auch numpy und matplotlib so gängig für die Auswertung von Daten ist, dass es bereits in der Anaconda-Distribution enthalten ist. Es muss aber natürlich sichergestellt werden, dass es importiert wird. Dies haben wir bereits in der ersten Code-Zelle dieses Kapitels oben mit dem gängigen Kürzel getan als import seaborn as sns.
Da seaborn auf matplotlib aufbaut, können wir die Funktionen von seaborn auch in Kombination mit matplotlib verwenden. Tatsächlich brauchen wir für unseren Fall jetzt nur plt.scatter() durch sns.swarmplot() ersetzen. Die Funktion sns.swarmplot() erwartet als Argumente ebenfalls x und y und zeichnet dann einen Dot-Plot. Wir können dies direkt für beide Personen A und B machen. Dabei verwenden wir wieder die Farben royalblue und orange, die wir bereits in den vorherigen Kapiteln verwendet haben. Außerdem wählen wir mit size=12 eine größere Punktgröße, da die standardmäßige Punktgröße in seaborn recht klein ist.
plt.figure()
plt.title('Person A')
sns.swarmplot(
x=pseudo_x,
y=noten_A,
color='royalblue',
size=12
)
plt.yticks(np.arange(1, 7))
plt.ylim(6.5, 0.5)
plt.ylabel('Note')
plt.xticks([])
plt.show()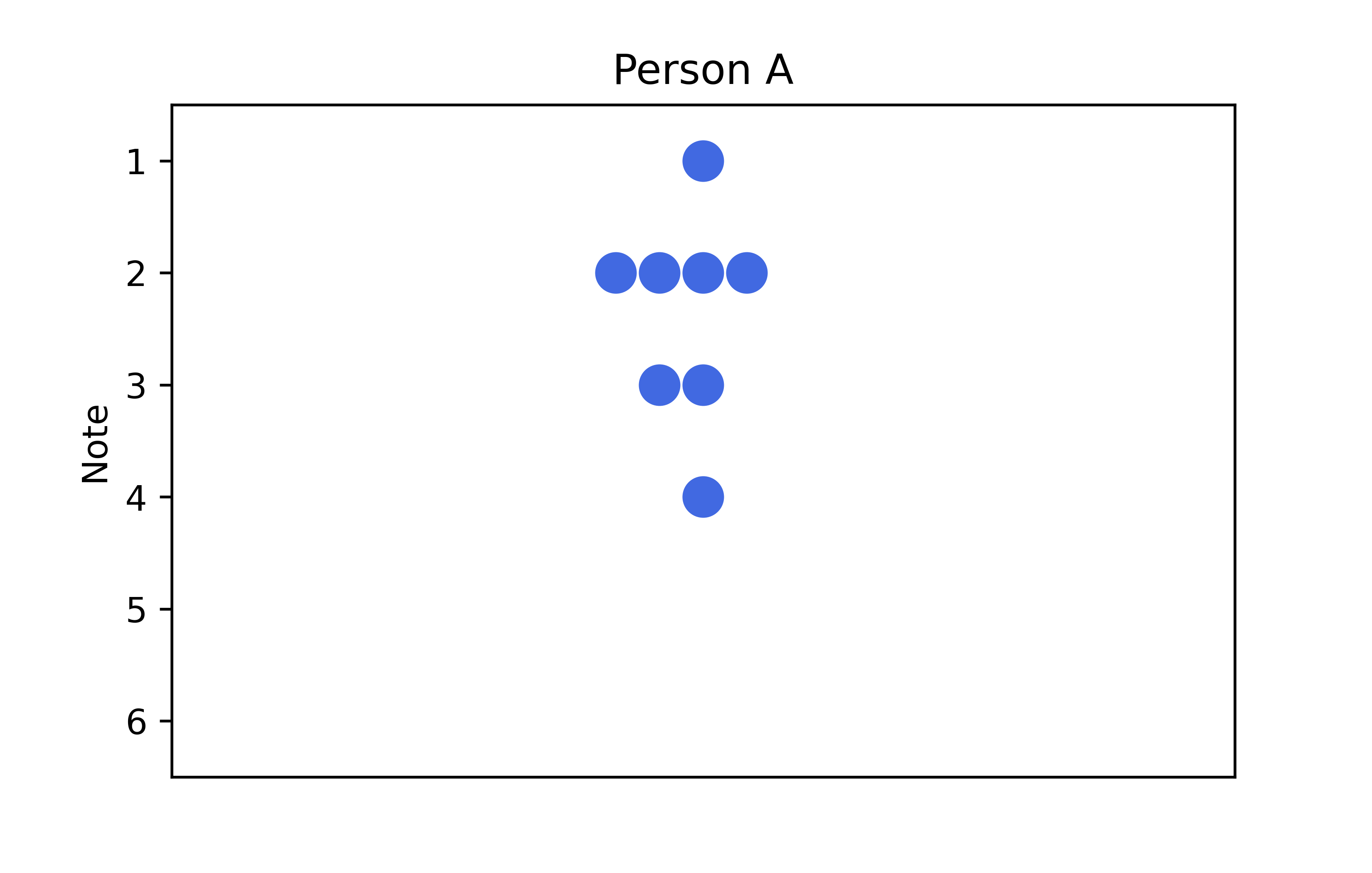
plt.figure()
plt.title('Person B')
sns.swarmplot(
x=pseudo_x,
y=noten_B,
color='orange',
size=12
)
plt.yticks(np.arange(1, 7))
plt.ylim(6.5, 0.5)
plt.ylabel('Note')
plt.xticks([])
plt.show()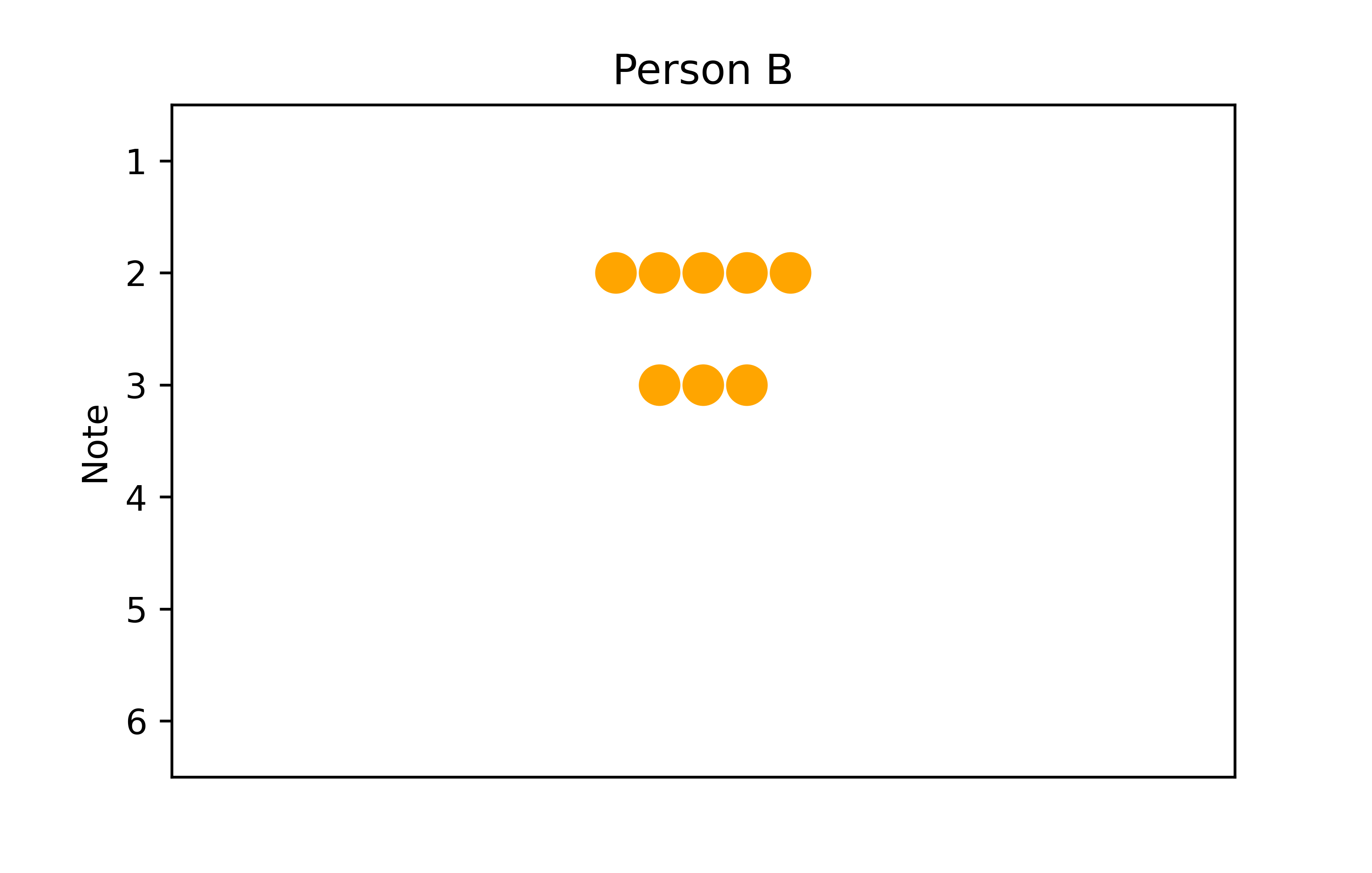
Das Ergebnis ist eindeutig besser. Wir sehen jetzt nicht nur wie viele vier verschiedene Noten die Personen hatte, sondern auch wie diese jeweils verteilt sind. Da unsere x-Achse hier keine Bedeutung hat ist es auch nicht problematisch, dass einige Punkte weiter links/rechts liegen als andere - das wäre natürlich anders, wenn auf der x-Achse auch eine numerische Variable abgebildet wäre wie in einem klassichen Streudiagramm.
Der Vorteil aller Punktdiagramme dieser Art ist, dass explizit und intuitiv verständlich jeder einzelne Wert im Datensatz dargestellt wird. Zumindest bei nicht allzu großen Datensätzen können so direkt die Lage, Verteilung, Anzahl und Ausreißer der Datenpunkte beurteilt werden.
Übungen
Erzeuge Dot-Plots für die Noten der Personen C und D und verwende dabei dieselben Farben, die in den entsprechenden Histogrammen des vorangehenden Kapitels verwendet wurden.
Versuche für mindestens eine Person deiner Wahl doch keinen Dot-Plot, sondern ein Streudiagramm mittels plt.scatter() zu zeichnen. Anstelle alle x-Werte auf 1 zu setzen, sollten sie hier aber auf 1, 2, 3, 4, 5, 6, 7 und 8 gesetzt werden. Dann kann auch der Befehle plt.xticks([]) weggelassen werden und stattdessen plt.xlabel('Reihenfolge') hinzugefügt werden. So entsteht ein Streudiagramm, das auch die Reihenfolge der Noten darstellt und so verhindert, dass die Punkte aufeinander liegen.
Fußnoten
Hin und wieder wird auch der Begriff “Punktdiagramm” speziell für Dot-Plots verwendet. In diesem Fall ist es wichtig, den Kontext zu beachten. In diesem Kapitel verwenden wir den Begriff “Punktdiagramm” im Allgemeinen für Diagramme mit Punkten bzw. Punkteverteilungen und “Dot-Plot” speziell für diese spezielle Form des Streudiagramms.↩︎